Um fio de cobre (de resistividade ) é usado para formar um anel de raio igual a . A área da seção reta do fio é de .
Os pontos e estão angularmente separados de , como mostra a figura.
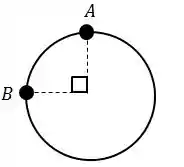
A resistência entre os pontos e é, aproximadamente:
;
;
;
;
Passo 1
Antes de sairmos calculando o valor de resistência, vamos dar uma olhada na nossa mesma figura novamente, imaginando que os pontos A e B estejam conectados por um fio externo:
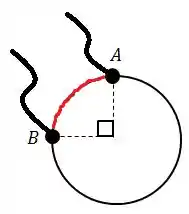
Reparem que temos 2 trechos (1 em vermelho e o outro em preto) para onde a corrente pode se dividir. Se formos simplificar o nosso desenho de acordo com os nossos desenhos de circuitos elétricos, teríamos algo parecido com:
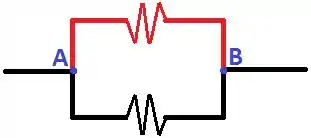
Desta forma, a resistência entre os pontos A e B é uma resistência equivalente calculada entre os trechos em vermelho e em azul. Vamos calcular essas resistências? ![]()
Passo 2
A resistência de um fio pode ser calculada por:
O problema já nos deu a resistividade e a área .
– Para o trecho em vermelho
Como os pontos e estão separados angularmente de , o comprimento será um quarto da circunferência de raio , logo:
– Para o trecho em preto
Como os pontos e estão separados angularmente de , o comprimento será da circunferência de raio , logo:
Passo 3
A área foi dada em , no entanto, precisamos passa-la para , dessa forma:
Passo 4
Dessa forma, a resistência para o trecho em vermelho será dada por:
Já a resistência para o trecho em preto será dada por:
Assim, nossa resistência será calculada como:
Assim, a opção que mais se aproxima é a letra .
Resposta
;