(Cap 26 Ex – 27) Dois condutores são feitos do mesmo material e têm o mesmo comprimento. O condutor A é um fio maciço de de diâmetro; o condutor B é um tubo oco com um diâmetro externo de e um diâmetro interno de . Qual é a razão entre as resistências dos dois fios, ? As resistências são medidas entre as extremidades dos fios.
Passo 1
E ai crianças, vocês estão prontos?
Estamos capitão!
Eu não ouvi direito!!
ESTAMOS CAPITÃO haha...
Bora resolveeeer
Temos dois fios feitos do mesmo material. O fio A tem de diâmetro e o fio B é oco com um diâmetro externo de e um diâmetro interno de , ambos com mesmo comprimento . Pela segunda lei de Ohm, podemos relacionar as resistências dessa forma:
Onde é a resistência, é a resistividade (que depende apenas do material), é o comprimento do fio e é a área da seção reta do fio.
Primeiramente, vamos determinar a área de cada fio. As duas áreas serão áreas de círculos, pois as seções retas dos fios são círculos. Isso porque temos um fio e o cortamos dessa forma:
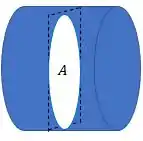
Logo, , como
Para o fio A, teremos exatamente a situação da imagem acima, então a seção reta será:

Agora, para o fio B, podemos calcular a área de um círculo com diâmetro e subtrair um círculo com o diâmetro . Pois ele tem esse cara aqui:
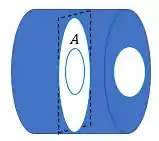
Logo, a seção reta é:
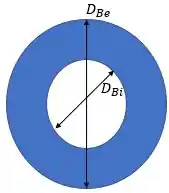
Então:
Passo 2
Agora, vamos voltar para a segunda lei de Ohm:
Portanto:
E
Como queremos a razão entre eles:
Podemos cortar o e o :
Substituindo os valores que temos:
Podemos cortar :
Substituindo os valores do enunciado:
Show! Fechamos mais uma!