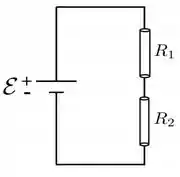
2 - Os resistores Ôhmicos 1 e 2 (com ) são conectados em série, através de fios ideais, a uma bateria de fem . Sabe-se que os resistores apresentam geometria cilíndrica com mesmos comprimento e área de seção reta: e . Sendo e as conduvidades dos materiais, e os campos elétricos no interior dos resistores, e as densidades de corrente nos resistores, é CORRETO afirmar que:
Passo 1
Bem, como os resistores estão conectados em séria, a corrente que passa nos dois é a mesma, certo?
A gente sabe que corrente está ligada a densidade de corrente através dessa integral de superfície aqui:
Para uma corrente na direção da área (Área transversal do resistor), como no desenho abaixo...
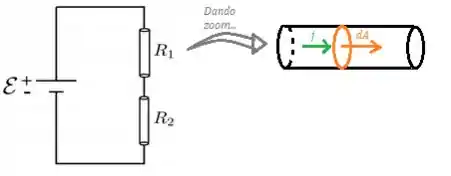
Nesse caso, o produto escalar entre a densidade de corrente e o vetor vira simplesmente o produto de por , afinal produto escalar de vetores de mesma direção nada mais é do que o produto dos módulos:
Então, a densidade de corrente está ligada a corrente a área da seção transversal. Como no nosso caso, tanto a área quanto a corrente são as mesmas em ambos os resistores, então certamente a densidade de corrente será igual nos dois:
Passo 2
Bem, sabemos que nos resistores, , e as resistências pode ser escrita em função da condutividade do material:
Perceba que é inversamente proporcional a . Como é constante nos dois resistores, para ser maior, a condutividade dele deve ser menor. Então...
Só está faltando falar sobre o campo magnético!
Passo 3
Bem, sabemos ainda que existe uma equação que uni tanto quanto e ainda o campo elétrico:
Como permanece constante, o campo elétrico tem que ser o oposto da condutividade. Ou seja, se a condutividade de é maior, o campo elétrico de deve ser menor, mantendo constante, saca?
Resposta
Letra E.