5 - Uma densidade de corrente uniforme circula através de um fio de comprimento quando conectado aos terminais de uma pequena bateria ideal com fem . Qual a resistividade ⍴ do material do fio?

Temos o valor da fem (a tensão ideal gerada pela pilha e que está atuando sobre o fio):

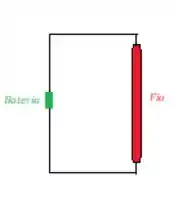
Sabemos que tensão se relaciona com o campo elétrico através da integral de linha:

No caso do fio condutor, o campo elétrico dentro dele na direção da corrente (para baixo). Assim como o (vetorzinho direcional que aponta o deslocamento das cargas):

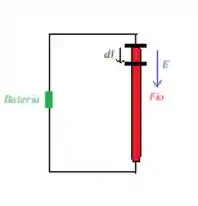
Sendo assim, como e tem o mesmo sentido, o produto vetorial entre eles fica sendo apenas o produto dos módulos:

Ora, a integral de é o comprimento todo do fio:

Lembre-se é a mesma coisa que . A punica diferença é que considera as perdas na bateria. Mas como ela é ideal, ela não tem perdas, saca?

Então, podemos encontrar agora a resistividade..