Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Resistência e Resistividade

Ver Teoria
Exercício 46123456789101112131415161718192021222324252627282930313233343536373839404142434445474849505152535455565758

Enunciado

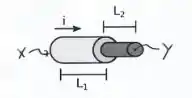
Os condutores 1 e 2 da figura abaixo são confeccionados de materiais diferentes. Os dois condutores têm comprimentos L 1 = 1,00   m e L 2 = 1,00   m , respectivamente. A resistividade e o diâmetro do condutor 1 são, respectivamente, ρ 1 = 2,0 × 10 - 6   Ω m e d 1 = 1,00   m m . A resistividade e o diâmetro do condutor 2 são ρ 2 = 1,0 × 10 - 6   Ω m e d 2 = 0,50   m m , respectivamente. Os dois condutores são unidos na forma mostrada na figura e são submetidos a uma corrente i = 2,0   A . Determine:

  1. A resistência de cada um dos condutores.
  2. A diferença de potencial entre as extremidades dos condutores (pontos x e y da figura abaixo).
  3. A potência total dissipada por ambos os dois condutores.

Passo 1

L e t r a   A :

FAAALA! Tudo bom? Vamos começar esse problema te falando que resistência de um cabo pode super ser encontrada usando a área da seção transversal, largura do cabo e resistividade do material:

R = ρ L A

Então, para o cabo 1 , a resistência será...

R 1 = ρ 1 L 1 A 1

E para o cabo 2...

R 2 = ρ 2 L 2 A 2

Passo 2

Tá! Mas quem são as áreas?

Cara... Como já mencionamos, elas são as áreas das seções transversais onde a corrente passa. É como se cortasse o fio por um plano e você vesse qual é a área desse plano que seria a seção:

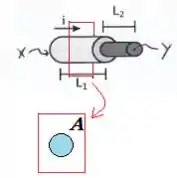
Como a área de um círculo é π r 2 onde r é a metade do diâmetro a área do cabo 1 vai ser...

A 1 = π d 1 2 4     →

A 1 = π 1,00   m m 2 4

Cara, m m representa milímetro onde mili nada mais é do que 10 - 3 de um metro. Logo...

A 1 = π 1,00 ⋅ 10 - 3 m 2 4       →

A 1 = π 10 - 6 m 2 4       →

A 1 = π 4 ⋅ 10 - 6   m 2

Então essa é a área da seção 1 em m 2 , para a seção 2, vamos repetir as continhas, mas considerando d 2 = 0,50   m m , ou seja, 1 2 m m ...

A 2 = π d 2 2 4

A 2 = π 1 2 ⋅ 10 - 3 m 2 4       →

A 2 = π 1 4 10 - 6 m 2 4       →

A 2 = π 16 ⋅ 10 - 6   m 2

Passo 3

Com as áreas das seções já calculadas, podemos então encontrar as resistências, voltando para onde paramos no passo 1:

R 1 = ρ 1 L 1 A 1             e                 R 2 = ρ 2 L 2 A 2

Substituindo então os dados na resistência 1 ...

R 1 = 2,0 × 10 - 6   Ω m   1,00   m π 4 ⋅ 10 - 6   m 2       →

R 1 = 2,0 × 10 - 6     1   m 2 π 4 ⋅ 10 - 6   m 2       Ω →

Simplificando...

R 1 = 2,0     1   π 4       Ω →

R 1 = 8 π       Ω →

O que vai nos dá aproximadamente...

R 1 = 2,55   Ω

Calculando agora para a resistência 2 ...

R 2 = ρ 2 L 2 A 2   →

R 2 = 1,0 × 10 - 6   Ω m   1,00   m π 16 ⋅ 10 - 6   m 2       →

R 2 = 1 , 0 × 10 - 6     1   m 2 π 16 ⋅ 10 - 6   m 2       Ω →

Simplificando...

R 2 = 1 , 0     1   π 16       Ω →

R 2 = 16 π       Ω →

O que vai nos dá aproximadamente...

R 2 = 5,09   Ω

Ou seja, R 2 = 2 R 1 .

Passo 4

L e t r a   B :

Cara, temos resistência e temos a corrente... Para encontrar a diferença de potencial então nos basta aplicar a Lei de Ohm:

V = R i

Mas atenção!

Queremos a diferença de potencial ente os pontos x e y :

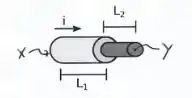
Como em cada fio temos uma resistência diferente, temos que calcular a diferença de potencial em cada fio e depois soma-las para obter a diferença de potencial total ( V x y ).

OBS: Pra você que já ta manjando bem circuitos, é como se considerássemos duas resistências em série, ta ligado?

Passo 5

Então primeiro vamos determinar a diferença de potencial para o cabo 1 :

V 1 = R 1 i   →

V 1 = 2,55 ⋅ 2

V 1 = 5,09   V

Agora, para o cabo 2 ...

V 2 = R 2 i

V 2 = 5,09   ⋅ 2   →

V 2 = 10,19   V

Sim! A corrente é mantida a mesma porque ela é a única que passa pelos dois fios.

Bem, a diferença de potencial então entre os pontos x e y será...

V x y = V 1 + V 2     →

V x y = 15,28   V

Passo 6

L e t r a   C :

POW! A potência dissipada pelos dos fios pode ser dada por...

p = V x y i

Então...

p = 15,28   ⋅ 2   →

p = 30,56   W

Legal, neh?

Resposta

Letra A:

R 1 = 2,55   Ω             e                 R 2 = 5,09   Ω

Letra B:

V x y = 15,28   V

Letra C:

p = 30,56   W

Exercícios de Livros Relacionados

Uma barra de alumínio de seção reta quadrada tem 1,3 m de comprimento e 5,2 m m de lado. (a) Qual é a resistência entre as extremidades da barra? (b) Qual deve ser o diâmetro de uma barra cilíndrica d
Os enrolamentos de cobre de um motor têm uma resistência de 50 Ω a 20 º C º quando o motor está frio . Depois de o motor trabalhar durante várias horas, a resistência aumenta para 58 Ω . Qual é a nova
Quando um fio de metal é aquecido, não é apenas a resistividade que muda; o comprimento e a área do fio também são afetados. De acordo com a equação R=ρ L / A , as três grandezas devem ser levadas em
Se o número que indica o calibre de um fio aumenta de 6, o diâmetro é dividido por 2; se o calibre aumenta de 1, o diâmetro é dividido por 2 1 / 6 (veja a tabela do Problema 4). Com base nessas inform
Na Fig. 26-29, uma corrente elétrica atravessa um tronco de cone circular reto de resistividade 731 Ω · m , raio menor a = 2,00 m m , raio maior b = 2,30 m m e comprimento L = 1,94 c m . A densidade d