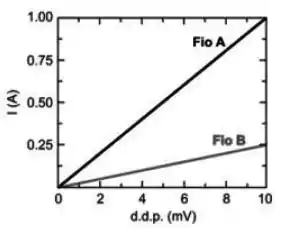
Considere dois fios condutores cilíndricos A e B de mesmo comprimento, feitos de um mesmo material e com diâmetros distintos. Para comparar as espessuras dos dois fios, mediu-se a corrente que atravessa cada fio como função da diferença de potencial à qual está submetido. Os resultados estão representados na figura. Analisando os resultados, conclui-se que a relação entre os diâmetros dos fios A e B é:
Passo 1
Bom, se temos um fio de resistividade , de comprimento e seção reta de área , então a sua resistência será:
Neste problema, temos dois fios que são feitos do mesmo material, por isso eles têm a mesma resistividade e mesmo , mas com áreas da seções retas cilíndricas diferentes. Por isso, primeiro precisamos calcular o valor da resistência de cada fio para depois usar a expressão acima e poder comparar os diâmetros e dos dois fios.
Olhando para o gráfico do Fio A, que é uma reta, podemos tirar o valor da resistência:
Repara que lá no gráfico, a resistência vai ser o inverso do coeficiente angular da reta! Fica ligado nisso, porque o gráfico é versus V!!
Fazendo a mesma coisa para o Fio B, teremos:
Passo 2
Agora, como o produto é o mesmo para os dois fios e área da seção reta de um cilindro é , com sendo o diâmetro, teremos o seguinte:
Simplificando essa expressão, teremos que:
Importante: para chegarmos a essa relação entre os diâmetros, foi fundamental que o problema falasse que os dois fios são feitos de mesmo material ( iguais) e tivessem o mesmo comprimento ( iguais). É por isso que é igual para os dois fios.
Resposta
Letra a.