UFRJ- Física 3 – P2 2018.1 - DIURNO - 3
Um fio condutor retilíneo é constituído por um cilindro condutor de raio e resistividade e uma casca cilíndrica condutora maciça de raio interno , raio externo () e resistividade , coaxial ao cilindro. Uma seção transversal deste é mostrada na figura abaixo. Sabendo que o fio é submetido a uma diferença de potencial constante entre suas extremidades, a razão entre as intensidades das densidades de corrente que fluem no cilindro e na casca cilíndrica vale:
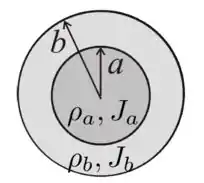
Passo 1
A questão não menciona, mas estamos lidando com dois condutores Ôhmicos, para os quais vale a relação para a densidade de corrente
em que é a condutividade do condutor, que é uma constante nesse caso, e é o campo elétrico aplicado ao condutor. Existe uma relação a condutividade e a resistividade que é a seguinte
Substituindo essa expressão naquela para , temos
Passo 2
Como o potencial entre as extremidades dos condutores é constante e esse condutores têm o mesmo comprimento , então podemos escrever que o módulo do campo elétrico é
Portanto, com essa expressão para , o módulo da densidade de corrente é
Passo 3
Aplicando a expressão anterior para cada condutor, teremos
Repara que a gente não precisou utilizar, explicitamente, dos raios e dos condutores para calcular a razão acima.
Resposta
Letra f).