Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo do Momento de Inércia em Corpos Extensos

Ver Teoria
Exercício 61234578910111213141516171819202122232425262728293031323334

Enunciado

Um balanço de parque é formado por uma barra cilíndrica de massa M , raio r , e comprimento L , preso por fios de massa desprezível a um eixo fixo superior, paralelo ao eixo da barra cilíndrica, conforme a figura ao lado. A barra pode girar em torno desse eixo fixo. O centro da barra está a uma distância d do eixo. O momento de inércia da barra com relação ao eixo fixo vale:

  1. M ( L 2 / 12 + d 2 )
  2. M r 2
  3. M d 2
  4. M ( r 2 / 2 + d 2 )
  5. M L 2 / 12

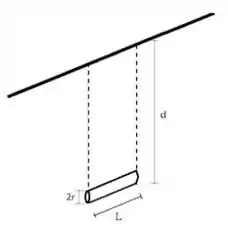
Passo 1

POW! Imagina se o eixo do balanço passasse em no eixo do cilindro de raio r ...

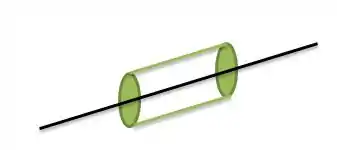
De acordo com a teoria, o momento de inércia do cilindro com relação a esse eixo que passa pelo centro de massa seria...

I C M = 1 2 M r 2

Então, para um eixo paralelo ao eixo do cilindro (como o eixo do balanço)...

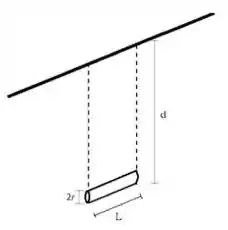
Podemos usar o teorema dos eixos paralelos! Vamos nessa?

Passo 2

O teorema dos eixos paralelos fala que se queremos o momento de inércia em relação a um eixo x e temos o momento de inércia em relação a um eixo y ...

Então...

I e i x o   x = I e i x o   y + M d 2

Considerando a nossa balança e o eixo y sendo o centro de massa...

I e i x o   x = I C M + M d 2   →

I e i x o   x = 1 2 M r 2 + M d 2   →

I e i x o   x = M r 2 2 + d 2

Resposta

Letra D.

Exercícios de Livros Relacionados

(a) Mostre que o momento de inércia de um cilindro maciço de massa M e raio R em relação ao eixo central é igual ao momento de inércia de um aro fino de massa M e raio R / 2 em relação ao eixo central
Use integração para determinar o momento de inércia de um disco fino uniforme de massa M e raio R em relação a um eixo do plano do disco que passa pelo seu centro. Confira sua resposta referindo à tab
Use integração para determinar o momento de inércia, em relação ao seu eixo, de um cone circular reto uniforme de altura H , raio da base R e massa M .
Um cilindro de massa M e raio R possui uma densidade que cresce linearmente a partir do seu eixo, ρ = α r , onde α é uma constante positiva. a) Calcule o momento de inércia do cilindro em relação a um
9.19E Calcule o momento de inércia de um cubo homogêneo de massa M e aresta a em relação a um eixo passando por uma de suas arestas.