Seja um corpo na forma de um quadrado de lado composto por hastes finas com massas indicadas na figura. Na figura está também indicado o sistema de coordenadas a ser utilizado. O corpo pode girar livremente sem atrito em torno do eixo e encontra-se em repouso na posição indicada.
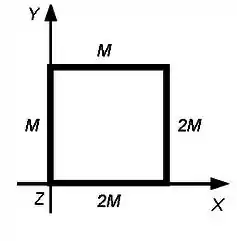
(a) Determine o momento de inércia rotacional do corpo em torno do eixo em função dos dados do problema.
Passo 1
O momento de inércia das hastes
Caramba, como que se calcula o momento de inércia de um quadrado vazado? Parece difícil não é? Mas calma, é mais simples do que parece. Ao invés de pensarmos em um quadrado, vamos pensar em cada uma das hastes:
Ou seja, o momento de inércia total vai ser a soma do momento de inércia das hastes perpendiculares ao eixo e das hastes paralelas ao eixo
Passo 2
O momento de inércia das hastes paralelas
Desenhando somente as hastes paralelas ao eixo de rotação, vamos ter:
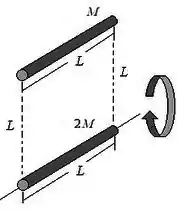
Para cada uma dessas hastes, o momento linear será:
Onde “” é a distância do centro de massa de cada uma dessas hastes para o eixo de rotação. Vamos ter então
Passo 3
O momento de inércia das hastes perpendiculares
Desenhando somente as hastes perpendiculares ao eixo de rotação, vamos ter:
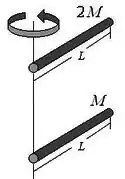
Para cada uma dessas hastes, o momento linear será
O momento linear perpendicular vai ser então:
Passo 4
O momento de inércia total
Agora é só aplicar o que já sabemos. Vamos ter:
Resposta
a)