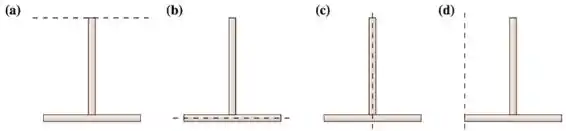
Duas barra idênticas de mesma massa e comprimento são usadas para desenhar um objeto com a forma de letra . O objeto pode girar em torno dos eixos indicados pela linha tracejada na figura. Para os momentos de inércia a , relacionados com a rotação em torno ao eixo indicado, pode-se afirmar que:
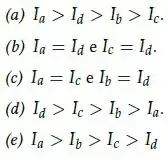
Passo 1
O momento de inércia é menor quando você tem mais massa concentrada perto do eixo, então que que a gente tem que fazer? Ver quais barras estão mais longe do eixo pra sabermos quais tem o momento de inercia maior
Resposta
Exercícios de Livros Relacionados
(a) Mostre que o momento de inércia de um cilindro maciço de massa M e raio R em relação ao eixo central é igual ao momento de inércia de um aro fino de massa M e raio R / 2 em relação ao eixo central
Use integração para determinar o momento de inércia de um disco fino uniforme de massa M e raio R em relação a um eixo do plano do disco que passa pelo seu centro. Confira sua resposta referindo à tab
Use integração para determinar o momento de inércia, em relação ao seu eixo, de um cone circular reto uniforme de altura H , raio da base R e massa M .
Um cilindro de massa M e raio R possui uma densidade que cresce linearmente a partir do seu eixo, ρ = α r , onde α é uma constante positiva. a) Calcule o momento de inércia do cilindro em relação a um
9.19E Calcule o momento de inércia de um cubo homogêneo de massa M e aresta a em relação a um eixo passando por uma de suas arestas.