Mostre que o momento de inércia de um cilindro de massa e raio em relação ao eixo central é igual ao momento de inércia de um aro fino de massa e raio em relação ao eixo central. Mostre que o momento de inércia de um corpo qualquer de massa em relação à qualquer eixo é igual ao momento de inércia de um aro equivalente em torno do mesmo eixo, se o aro tiver a mesma massa e um raio dado por
O raio do aro equivalente é chamado de raio de giração do corpo.
Passo 1
Aprendemos que o cálculo do momento de inércia de corpos extensos é feito por meio de integral, então, a primeira idéia é calcular a integral:
Certo?
Desespero bateu aí né?
Relaxa que papai aqui vai te passar o bizu. O bizu do estripador.
“Estripador? Que que é isso?!”
É aquele cara que faz parte por parte, bem devagar e com calma, então vamos lá!
Passo 2
A primeira coisa a se fazer é calcular o momento de inércia do aro homogêneo de massa e raio , em relação ao eixo central do mesmo.
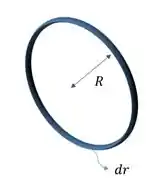
Aqui podemos usar a integral, pois trata-se de uma integral simples, saca só:
No aro, todas as minipartículas que o compõem estão à mesma distância do eixo de rotação, portanto:
Podemos concluir:
Passo 3
Beleza! Agora, vamos calcular o momento de inércia do cilindro em relação ao eixo central. Vamos considerar um elemento da forma de cilindro no interior do cilindro de massa , raio e comprimento . Esse elemento cilíndrico tem massa , raio e altura , como na figura abaixo.

Devemos considerar também que o cilindro possui uma densidade volumétrica uniforme, de forma que:
Assim, temos que o momento de inércia do cilindro maior pode ser obtido integrando o elemento infinitesimal para de 0 até :
Substituindo pela expressão obtida acima:
Substituindo por :
Passo 4
Agora que já temos o momento de inércia do cilindro e o momento de inércia do aro em relação ao eixo central, vamos voltar ao enunciado.
O momento de inércia de um cilindro de massa e raio é dado por:
O momento de inércia de um aro de massa e raio é dado por:
Logo, eles são iguais! :)
Passo 5
Vamos lá, estamos quase acabando!
Agora o que ele quer que a gente mostre é que o momento de inércia de um corpo de mass em relação a qualquer eixo é igual ao momento de inércia de um aro equivalente de massa e um raio ao redor desse mesmo eixo. Parece complicado, né? Vamos com calma!
Passo 6
Bom, já vimos que o momento de inércia de um aro em relação ao eixo central é dado por:
onde é o raio. Se é dado por , onde é o momento de inércia de um corpo em relação ao mesmo eixo, temos que:
Logo, mostramos que o momento de inércia de um corpo qualquer em relação a um dado eixo é igual ao momento de inércia de um aro em volta desse eixo de raio .
Resposta
Ei, a resposta está no passo a passo :)