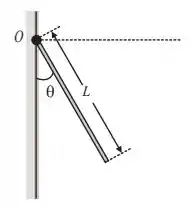
Uma barra homogênea de comprimento e massa está presa em uma de suas extremidades a uma parede vertical, conforme a figura ao lado. A barra gira sem atrito ao redor do ponto , sendo abandonada na posição horizontal com velocidade inicial nula. O momento de inércia da barra em relação ao ponto é e a aceleração da gravidade local é . No instante em que a barra faz um ângulo com a vertical, a aceleração angular da barra é:
Passo 1
Podemos tirar a informação da aceleração angular pela fórmula...
Onde é a informação de torque, é o momento de inércia e finalmente a nossa aceleração angular.
BELEZA! Então repare que se conhecermos o valor do torque, a gente pode tirar a aceleração angular através de...
Então é isso que vamos fazer! Buscar o valor do torque .
Passo 2
POW! O problema nos disse que nos vamos pegar a haste, levar ela até a posição horizontal e depois soltar. Não sei se você concorda comigo, mas a única força que vai existir na haste nesse momento é a força peso apontada para baixo e é a força que vai “puxar” a haste a fazendo girar:
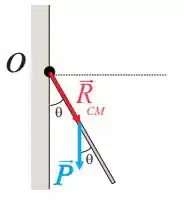
Mas uma pergunta interessante a se fazer aqui: Onde a força peso está aplicada? Em outras palavras... Quem é à distância (módulo do vetor , ou )?
Sabemos que a força peso é a única força na haste, logo é a força resultante. E tipo... A força resultante sempre vai está agindo no centro de massa do corpo. Se o nosso corpo é uma haste de comprimento ... O centro de massa vai ser o ponto central dela () de modo que...
De acordo com a nossa teoria, o torque causado por essa força peso na haste pode ser dado por...
Ou, em termos de módulo...
O peso da haste é a massa de toda a haste vezes a gravidade...
Se a haste estiver a com a vertical...
Passo 3
BELEZA!!! Temos o valor do torque da haste. Para encontrar a aceleração então como vimos no passo 1...
Simplificando...
Resposta
LETRA B.