UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 4 - Rotação, rolamento e corpos rígidos, Questão 2
Uma ruela padrão tem um raio interno e um raio externo de . A ruela tem espessura de . A densidade da liga metálica da ruela é Calcule o momento de inércia da ruela para um eixo que passa pelo seu centro e perpendicular ao plano dela.
Passo 1
Oii gente, tudo bom?
Nessa questão temos uma ruela, que é como uma coroa circular, mas que possui espessura. O raio interno dessa coroa vale:
E, o raio externo vale:
Além disso, a sua espessura vale e a sua densidade vale .
O objetivo é que calculemos o momento de inércia da ruela com relação a um eixo que passa pelo seu centro e é perpendicular ao seu plano.
Então pessoal, pra começar vamos dar uma revisada na definição de momento de inércia.
onde é a distância de cada elemento de massa até o eixo considerado.
Pra conseguir eliminar esse da jogada e resolver a integral, vamos a densidade volumétrica dada pra mudar nossa integral pra e depois para , beleza?
Vem comigo!
Passo 2
Bom, temos que resolver a integral:
Para resolvê-la devemos usar a densidade volumétrica da ruela, que sabemos que vale:
Assim, substituindo na integral, caímos no seguinte problema:
Show! Mas, essa integral com ainda não é trivial de ser calculada, então temos que tirá-la da jogada. Como a superfície plana da ruela é uma coroa circular, se tomarmos um elemento com espessura e parte plana também sendo uma coroa circular, vamos ter:
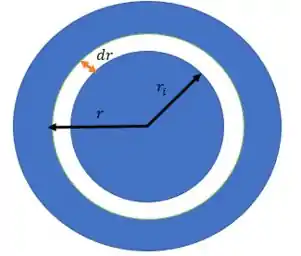
onde:
Substituindo tudo isso na integral, teremos:
Colocando as constantes pra fora, ficamos com:
Logo:
Pelo enunciado, temos que:
Substituindo, temos:
Portanto, fazendo essas continhas de cabeça (claro que não haha), temos:
E é isso pessoal! Espero que vocês tenham curtido a solução!
Até a próxima 😊