Considere uma partícula de massa girando em torno de um ponto com velocidade angular e raio , um anel de raio e massa total girando em torno de seu eixo de simetria com a mesma velocidade angular, e um disco de massa total girando em torno de seu eixo de simetria com a mesma velocidade angular. Se os momentos de inércia da partícula, do anel e do disco forem iguais a e , respectivamente, assinale a resposta certa:
A.
B.
C. .
D.
E.
Passo 1
Vamos enteder o que ele tá falando:
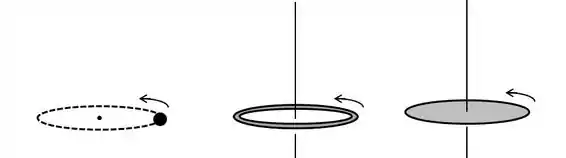
Pra gente calcular o momento de inércia de uma partícula girando em torno do ponto, usamos que:
O momento de inércia do anel e do disco são tabelados e dados.
Como todos possuem mesma massa e raio, então:
Suave na nave? De boa na lagoa!
Resposta
Alternativa D
Exercícios de Livros Relacionados
(a) Mostre que o momento de inércia de um cilindro maciço de massa M e raio R em relação ao eixo central é igual ao momento de inércia de um aro fino de massa M e raio R / 2 em relação ao eixo central
Use integração para determinar o momento de inércia de um disco fino uniforme de massa M e raio R em relação a um eixo do plano do disco que passa pelo seu centro. Confira sua resposta referindo à tab
Use integração para determinar o momento de inércia, em relação ao seu eixo, de um cone circular reto uniforme de altura H , raio da base R e massa M .
Um cilindro de massa M e raio R possui uma densidade que cresce linearmente a partir do seu eixo, ρ = α r , onde α é uma constante positiva. a) Calcule o momento de inércia do cilindro em relação a um
9.19E Calcule o momento de inércia de um cubo homogêneo de massa M e aresta a em relação a um eixo passando por uma de suas arestas.