Um pêndulo (vide figura) possui uma haste de comprimento e massa . Em sua extremidade inferior há um disco de massa e raio , cuja borda está colada na extremidade inferior da haste. A extremidade superior da haste pode girar em torno de um eixo sem atrito que permite o conjunto haste-disco oscilar.
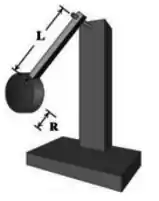
Haste: ; Disco:
a) Obtenha uma expressão literal para o momento de inércia do conjunto haste-disco em relação à extremidade superior da haste.
Passo 1
O momento de inércial do conjunto será a soma dos momentos de inércia da haste e do disco, ambos com relação ao eixo da extremidade superior da barra:
Vamos calcular cada um desses momentos de inércia.
Passo 2
Sabemos que o momento de inércia de uma haste com relação à um eixo perpendicular passando pelo seu centro de massa é:
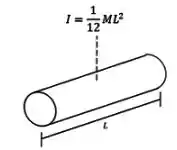
Porém, o eixo está passando pela extremidade da barra.
Então, vamos usar o teorema dos eixos paralelos:
A distância entre os eixos será metado do comprimento da haste:
Passo 3
O momento de inércia de um disco com relação a um eixo passando pelo seu centro de massa é:
Porém, novamente, o nosso eixo não está passando pelo centro de massa do disco, então vamos usar o teorema dos eixos paralelos de novo.
Quanto vale a distância entre os eixos?
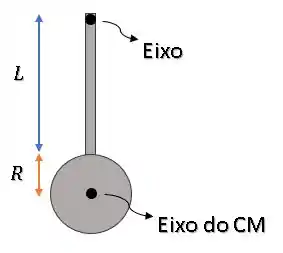
Então, temos:
Passo 4
Agora, basta somarmos os momentos de inércia:
Resposta
(a)