Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo do Momento de Inércia em Corpos Extensos

Ver Teoria
Exercício 20123456789101112131415161718192122232425262728293031323334

Enunciado

UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 4 - Rotação, rolamento e corpos rígidos, Questão 1

Disco fino e uniforme de massa M e raio R está montado sobre um eixo passando através de seu centro e perpendicular ao plano do disco. Determine o momento de inércia sobre dois eixos paralelos e perpendiculares ao plano do disco

  • O próprio eixo passando pelo centro do disco.
  • Um eixo passando nas bordas do disco.

Passo 1

Fala aí pessoal, tudo bem com vocês?

Nessa questão temos um disco uniforme (possui densidade constante), considerado plano, que possui massa total M e raio R . Precisamos calcular o momento de inércia em relação ao eixo que passa perpendicularmente ao centro do disco, e a um eixo que passa pelas bordas.

E aí, o que podemos fazer aqui?

Então pessoal, pra começar vamos dar uma revisada na definição de momento de inércia.

I = ∫ r 2 d m

onde r é a distância de cada elemento de massa d m até o eixo considerado.

Puts, mas como vamos integrar d m ? Aí é que entra a história do disco ser uniforme, por causa disso poderemos usar a ideia de densidade pra cada elemento de massa d m , e assim escrevê-los em função de r .

Show de bola!

Pra calcular no outro eixo, podemos usar também o teorema dos eixos paralelos. Basicamente, ele diz que:

I e 1 = I O + m ⋅ d 2  

onde d é a distância entre os eixos e 1 e e 2 , O é o eixo que perpendicular ao centro de massa do objeto, e e 1 é um eixo paralelo ao primeiro.

Massa! Vamo nessa!!

Passo 2

Bom pessoal, vamos começar calculando o momento de inércia com relação ao eixo que passa pelo centro do disco, beleza?

Isso facilita um pouco, pois a distância de cada elemento de massa d m que está em uma mesma circunferência do disco, é a mesma.

Temos:

I = ∫ r 2 d m

Mas, podemos escrever que:

ρ = d m d A

onde ρ é a densidade superficial de massa. Daí, substituindo no momento de inércia, temos:

I = ρ ⋅ ∫ r 2 d A

Beleza?!

Puts, mas d A ainda não ajuda muito a resolver a integral. Vamos então considerar o seguinte na nossa integração:

Tomamos pequenas coroas circulares ao longo do disco, até compor todo o disco. Essas coroas estão a uma distância r do centro do disco, e possuem espessura d r . Assim, a sua área vai valer:

d A = 2 π r ⋅ d r

onde 2 π r é o comprimento dessa coroa.

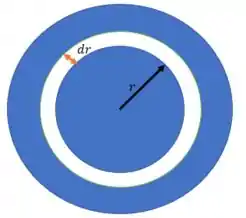
Logo, substituindo na integral, vamos ter:

I = ρ ∫ r 2 ⋅ 2 π r d r

= 2 π ρ ∫ r 3 d r

No caso, precisamos pegar coroas circulares que varram toda a área do disco. Ou seja, precisamos que:

0 ≤ r ≤ R

Assim, finalmente temos a nossa integral prontinha pra ser calculada:

I = 2 π ρ ∫ 0 R r 3 d r

Boaa!

Passo 3

Agora vamos resolver a integral:

I = 2 π ρ ∫ 0 R r 3 d r

= 2 π ρ ⋅ r 4 4 0 R

= 2 π ρ ⋅ R 4 4

Logo:

I = π ρ R 4 2

Mas, o enunciado não deu ρ pra gente certoo?

Mais ou menos, ele deu a densidade indiretamente, pois sabemos que a massa do disco vale M e o raio vale R , logo:

ρ = M A = M π R 2

Substituindo, vem que:

I = π ⋅ M π R 2 ⋅ R 4 2

Portanto, encontramos que o momento de inércia com relação ao eixo que passa pelo centro do disco vale:

I O = M R 2 2

Excelente!

Passo 4

Pra calcular o momento de inércia com relação ao eixo que passa pela borda, vamos utilizar o Teorema dos eixos paralelos. Assim:

I e = I o + M d 2

Como a distância da borda do disco até o seu centro vale R , vamos ter:

I e = I O + M R 2

= M R 2 2 + M R 2

∴ I e = 3 M R 2 2

Resposta

I O = M R 2 2

I e = 3 M R 2 2

Exercícios de Livros Relacionados

(a) Mostre que o momento de inércia de um cilindro maciço de massa M e raio R em relação ao eixo central é igual ao momento de inércia de um aro fino de massa M e raio R / 2 em relação ao eixo central
Use integração para determinar o momento de inércia de um disco fino uniforme de massa M e raio R em relação a um eixo do plano do disco que passa pelo seu centro. Confira sua resposta referindo à tab
Use integração para determinar o momento de inércia, em relação ao seu eixo, de um cone circular reto uniforme de altura H , raio da base R e massa M .
Um cilindro de massa M e raio R possui uma densidade que cresce linearmente a partir do seu eixo, ρ = α r , onde α é uma constante positiva. a) Calcule o momento de inércia do cilindro em relação a um
9.19E Calcule o momento de inércia de um cubo homogêneo de massa M e aresta a em relação a um eixo passando por uma de suas arestas.