O momento de inércia de uma barra reta homogênea em relação a um eixo perpendicular a ela e ao plano do papel e que passa pelo seu centro de massa vale . Num dado instante a barra é dobrada em torno de seu ponto médio de maneira que assuma a forma de um “V” cujo ângulo de abertura é . O momento de inércia da barra dobrada em relação ao mesmo eixo é
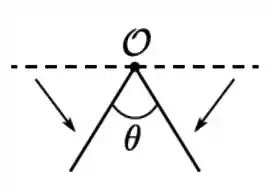
(a)
(b)
(c)
(d)
(e)
Passo 1
A gente calcula o momento de inércia fazendo
pra uma partícula, ou
pra um corpo extenso.
A ideia é que o momento de inércia é proporcional à massa e ao quadrado da distância dessa massa ao eixo.
Passo 2
Vamos considerar um pedacinho da barra, uma partícula de massa e distância ao eixo :
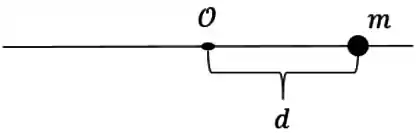
Então o momento de inércia dessa partícula em relação ao eixo é .
Passo 3
Quando a barra dobra, a massa da partícula não muda, é claro. O lance é perceber que a distância ao eixo também não muda! Saca:
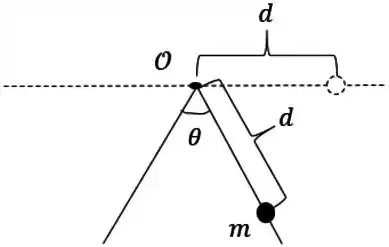
Passo 4
Isso significa que o momento de inércia da partícula em relação ao eixo continua o mesmo, valendo . Pegamos uma partícula genérica da barra, então isso vale pra qualquer uma!
Portanto, o momento de inércia total da barra em relação ao eixo continua o mesmo, .
Passo 5
Alternativa (a)
Resposta
Ei, a resposta está no passo a passo :)