PUCRIO, Álgebra Linear I, G1-2017.1, Questão 1b,c,d
Considere as retas em
e .
(b) Calcule a distância entre as retas e .
(c) Determine a posição relativa entre as retas e .
(d) Determine uma equação paramétrica da reta que liga os dois pontos mais próximos de e , ou seja, a reta com as seguintes propriedades:
(i) ;
(ii) ;
(iii) e são concorrentes;
(iv) e são concorrentes.
Passo 1
Para começar, na letra (b) vamos tentar visualizar essa situação aí, lembrando que pra calcular a distância entre retas temos que ligar as duas por uma reta que seja perpendicular às duas. Dessa forma:
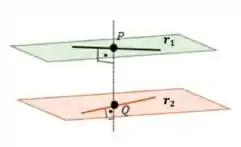
E medir o tamanho, ou seja, módulo do vetor !
Bom, vamos listar o que já sabemos esse vetor :
- Sua origem é um ponto de e sua extremidade é um ponto de
- Ele é ortogonal ao vetor diretor de e , ou seja, e
Vamos aplicar isso aí então, primeiro achamos o vetor genérico :
Agora vamos fazer o produto interno desse vetor com os vetores diretores de cada reta:
Agora é só resolver o sistema:
E assim achamos e .
Substituindo, vamos achar nosso vetor:
Pra terminar, agora, é só calcular o seu módulo:
Passo 2
Na letra (c), para saber a posição relativa das retas, fazemos o determinante do produto misto do vetor sendo e
Se der zero, as retas são coplanares, aí podem ser paralelas, coincidentes ou concorrentes, mas, se não der zero, indica que as retas são reversas.
Mãos a obra:
Opa, deu diferente de zero, logooo, as retas só podem ser reversas.
Passo 3
Essa reta que queremos na letra (d) é a gerada pelo vetor que liga perpendicularmente os dois planos, ou seja,
Para achar a equação paramétrica só preciso de um vetor diretor (que já tenho, ) e um ponto, o qual posso escolher ou
Escolhendo minha reta fica com essa cara:
Resposta
(b)
(c) Retas reversas
(d)