UTFPR, sem campus, Geometria Analítica e Álgebra Linear, P1, 2018.1, questão 2b
Determine a distância entre as retas abaixo:
b)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma reta e uma reta e pediu pra gente determinar a distância entre elas. Como as duas não tem componente na direção , nós podemos dizer que elas pertencem ao e, portanto, estão no mesmo plano, certo?
Mas será que elas são paralelas ou concorrentes? Nós sabemos que duas retas são paralelas, se poderem ser escritas na forma , ou seja, se forem proporcionais. Se , dizemos que as retas são concorrentes. Onde e são os vetores diretores da reta.
Como as nossas equações da reta estão na forma geral:
O que nós vamos fazer escolher dois pontos aleatórios para e , encontrar seus vetores diretores e, a partir daí, verificar se as retas são paralelas ou concorrentes e a distância entre elas.
Escrevendo as nossas equações no formato vetorial, fica mais fácil enxergar esses vetores diretores:
Vamos lá!
Passo 2
Vamos começar escolhendo um ponto aleatório para , fazendo :
E isolando :
Em seguida, vamos fazer e consequentemente:
Assim, temos os pontos e na reta .
De mesma forma, vamos chamar na reta :
Fazendo agora :
E temos os pontos e na reta .
Passo 3
Para encontrar seus vetores diretores, vamos usar os pontos que encontramos no passo anterior. Fazendo:
E
Assim, temos o vetor diretor e o vetor diretor .
Agora precisamos testar se eles são paralelos ou concorrentes, usando a equação:
Temos:
Se abrirmos isso, ficamos com:
Como os valores de não batem, nossas retas só podem ser concorrentes. E quando as retas são concorrentes, a distância entre elas é zero. O que faz sentido, já que as retas se cruzam, olha só:
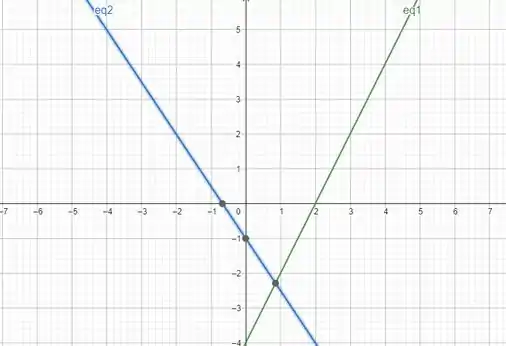
É isso aí, galera. Até a próxima! 😉