Sejam e retas distintas em . Considere as seguintes afirmações:
A distância entre e será igual a zero, se e somente se, e forem concorrentes;
se e forem paralelas, então para qualquer ponto , valerá que a distância entre e será igual à distância entre e ;
se e forem reversas, então para qualquer ponto , valerá que a distância entre e será igual à distância entre e .
Assinale a alternativa correta:
a) todas as afirmações são necessariamente verdadeiras;
b) apenas a afirmação é necessariamente verdadeira;
c) apenas as afirmações e são necessariamente verdadeiras;
d) apenas as afirmações e são necessariamente verdadeiras;
e) apenas a afirmação é necessariamente verdadeira.
Passo 1
Fala aí pessoal, tudo certinho?
Nessa questão precisamos avaliar afirmações acerca da distância entre ponto e reta, e entre reta e reta. Algo muito importante é que o enunciado fala que e são distintas.

Na afirmação é dito que a distância entre e é nula se, e somente se, e forem concorrentes.
Nesse caso, temos uma condição de “se, e somente se”. Isso significa que precisamos provar tanto a ida como a volta:
- ida Se e forem concorrentes, a distância entre e é nula
De fato, sendo e concorrentes, elas possuem um ponto em comum. Como a distância entre duas retas é dada pela menor distância possível entre dois pontos da reta, esse ponto será justamente o ponto em comum e a distância é nula.

- Volta : Se a distância entre e for nula, e são concorrentes.
Realmente, para que a distância entre duas retas seja nula só existem duas possibilidades. Ou elas são coincidentes, ou são concorrentes. O enunciado fala que e são distintas, portanto, elas precisam ser concorrentes.
Prontinho! A afirmação é verdadeira.
Passo 2
A afirmação basicamente diz que se e são paralelas, a distância entre as retas é dada pela distância entre qualquer ponto de até a reta .
Para avaliar essa afirmação, podemos lembrar que a distância entre um ponto e uma reta é dada pela distância entre um ponto fora da reta e a sua projeção. Assim:
Onde .
Mas, como e são paralelas, a distância entre elas é dada justamente por um ponto pertencente a uma das retas e a sua projeção na outra reta. Assim:
Logo, concluímos que:
E, a afirmação também é verdadeira.
Passo 3
A afirmação afirma que se e são reversas, a distância entre e é dada pela distância de qualquer ponto até .
Nesse caso, podemos tentar visualizar um exemplo pra avaliar se a afirmação é verdadeira.
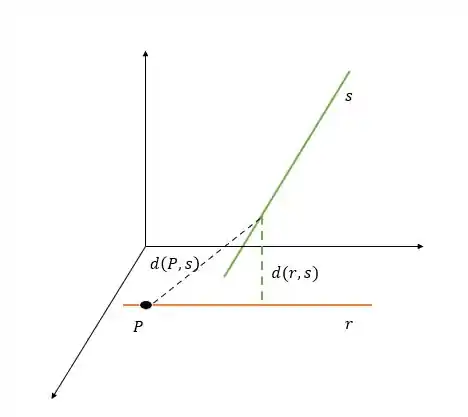
Na imagem acima temos e reversas. .
Porém, a distância entre e é dada pela distância entre e sua projeção na reta . Mas, a distância entre e é dada exclusivamente pelo par de pontos que são a projeção de em e de em .
Assim, na imagem ficou nítido que a distância entre e não é a menor distância possível entre dois pontos de e . Portanto, a afirmação é falsa.
Logo, a resposta é a letra c).
É isso gente, obrigado pela atenção.
Resposta
Letra c).