Associe cada quádrica ao gráfico que mais se assemelha a ela:
i) 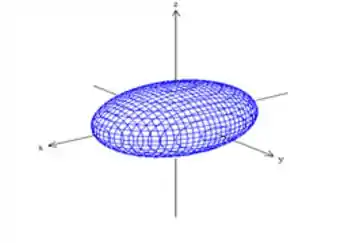
ii) 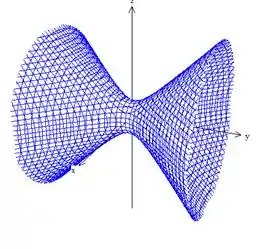
iii) 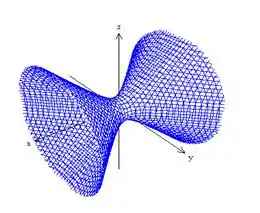
iv) 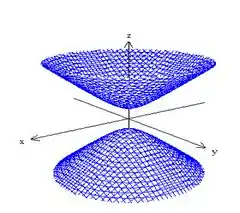
v) 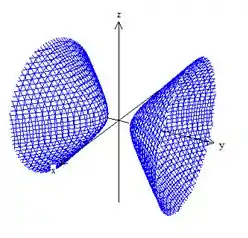
Passo 1
Antes de começar, só um obszinho: tem 5 figuras e 4 opções apenas, estranho, né? Mas é que alguma opção de superfície vai se aplicar a mesma figura, ou seja, uma mesma figura vai estar associada a mais de uma superfície. Pode parecer estranho a questão fazer isso, mas a ideia era só ver se a gente conhece a “cara” das superfícies.
Sem mais delongas, vamos lá: devemos observar os sinais dos coeficientes que estão multiplicando as variáveis elevadas ao quadrado.
- 3 coeficientes positivos, isso indica uma elipsoide
- 2 coeficientes positivos, indica uma hiperboloide de uma folha
- 2 coeficientes positivos, indica uma hiperboloide de uma folha
- 3 coeficientes positivos, isso indica uma elipsoide
Passo 2
Devemos agora conseguir colocar as equações das quádricas na forma geral de cada uma delas, para termos certeza que são essas quadricas mesmo.
- , dividindo por 10 temos: isso confirma que trata-se de um elipsoide.
- , é um hiperboloide de uma folha
- , é um hiperboloide de uma folha
- é um elipsoide
Passo 3
Agora vamos correlacionar as quádricas já identificadas com seu esboço
- É um elipsoide, portanto a única alternativa possível é a i)
- É um hiperboloide de uma folha com o coeficiente de negativo. Seu gráfico só pode ser a alternativa iii)
- É um hiperboloide de uma folha com o coeficiente de negativo. Seu gráfico só pode ser a alternativa ii)
- É um elipsoide, portanto a única alternativa possível é a i)
Resposta
- Elipsoide, figura i)
- Hiperboloide de uma folha, figura iii)
- hiperboloide de uma folha, figura ii)
- Elipsoide, figura i)