e
Identifique e esboce as superfícies e .
Passo 1
Identificar :
Temos dois sinais negativos:
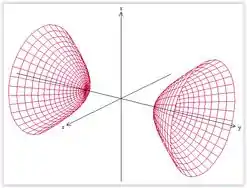
Logo, a superfície é um hiperboloide de duas folhas e o eixo está em , pois é o termo positivo na equação.
Passo 2
Esboço de :
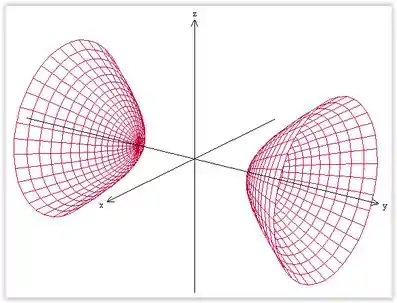
Passo 3
Identificar :
Temos um sinal negativo:
Logo, a superfície é um hiperboloide de uma folha e o eixo está em , pois é o termo negativo na equação.
Passo 4
Esboço de :
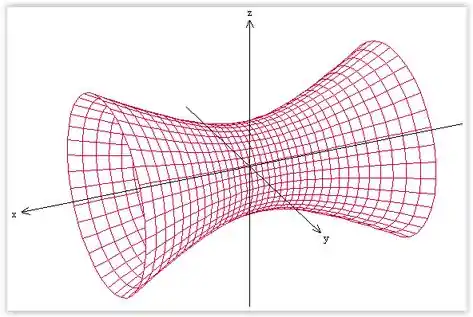
Resposta
é hiperboloide de duas folhas.
é hiperboloide de uma folha.
Esboços: