Superfícies
Seja a quádrica cuja equação cartesiana é dada por .
Identifique a quádrica.
Passo 1
Identificar a quádrica:
A equação da quádrica tem termos e .
Portanto, precisamos completar quadrados:
Comparando termo a termo:
Resolvendo o sistema, encontramos que:
Passo 2
Voltando à equação da quádrica e somando nos dois lados:
Dividindo tudo por :
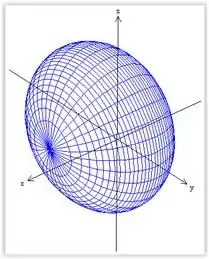
Logo, essa quádrica é um elipsoide com centro em .
Resposta
Elipsoide com centro em .
Exercícios de Livros Relacionados
Os Exercícios 25 e 26 nos dão informações sobre os focos e vértices das elipses centradas na origem do plano xy. Em cada um dos casos, encontre a equação na forma padrão da elipse a partir das informa
Os Exercícios 49-52 fornecem equações para elipses e nos dizem quantas unidades para cima ou para baixo e para a direita ou para a esquerda cada elipse deve ser deslocada. Encontre uma equação para a
Os Exercícios 27-34 fornecem equações para hipérboles. Coloque cada equação na forma padrão e encontre as assíntotas da hipérbole. Em seguida, esboce a hipérbole. Inclua as assíntotas e focos no seu e
Os Exercícios 53-56 fornecem equações para hipérboles e nos dizem quantas unidades para cima ou para baixo e para a direita ou para a esquerda cada hipérbole deve ser deslocada. Encontre uma equação p
Os Exercícios 27-34 fornecem equações para hipérboles. Coloque cada equação na forma padrão e encontre as assíntotas da hipérbole. Em seguida, esboce a hipérbole. Inclua as assíntotas e focos no seu e