UTFPR, Sem Campus, Cálculo Diferencial e Integral 2, Listas de Cáclulo 2 - Profº Félix Gómez - Primeira Lista, Questão 1.2a
2] Cada uma das seguintes inequações determina um conjunto de pontos em e . Identificar as bolas abertas e as bolas fechadas identificando o centro e seu raio.
(a)
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema serão dadas inequações de esferas ou círculos e nosso objetivo é identificar o centro e o raio da esfera ou do círculo.
Ok, mas como podemos descobrir isso? 👀
A inequação genérica da esfera é dada por
Onde , e são as coordenadas do centro da esfera e é o raio da esfera.
Já a inequação do círculo é a mesma coisa só que excluindo o termo
Sacou? Bora lá! 😉
Passo 2
A inequação dada é
Então temos que manipular essa inequação para ser escrita como uma das inequações do passo 1.
Nesse caso não temos a coordenada , então se trata de um círculo.
O termo é o único termo que contém a variável , portanto podemos dizer que o centro do círculo em está em .
Já o termo aparece em e .
Como , podemos comparar com e ver que e ...
Ou seja, essa inequação se trata de um círculo de raio e centro em
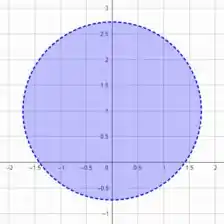
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
Círculo de raio e centro em .