Considere a função
Seja a superfície de nível de passando pelo ponto e seja a superfície dada pela equação
Dentre as superfícies, temos:
- Um cone com vértice no ponto
- Dois planos contendo o eixo e um elipsóide centrado no ponto
- Um parabolóide hiperbólico
- Um cilindro e uma esfera centrada no ponto
- Um hiperbolóide de duas folhas
Passo 1
Precisamos desvendar o que essas superfícies aí são.
Vamos começar pela primeira, que é a superfície de nível de que passa pelo ponto , ou seja
Assim, a nossa superfície nada mais é que
E o que diabos é isso??
Passo 2
Vamos pensar com calma!
Se fosse
A gente saberia que isso é um plano, certo? No a gente tem uma reta, mas como estamos do , então se o não aparece é porque ele pode ser qualquer coisa, então, temos um plano que contém o eixo .
Ok, mas ai o que que acontece quando a gente eleva os dois lados ao quadrado?
Antes nós tínhamos que tem o valor de exatamente igual ao valor de . Agora, como temos tudo ao quadrado, o que pode acontecer é que se o , o pode ser igual a ou igual a porque no fim das contas teremos . E vice versa.
Então o que acontece é que agora em vez de um plano só, nós temos dois planos contendo o eixo , assim:
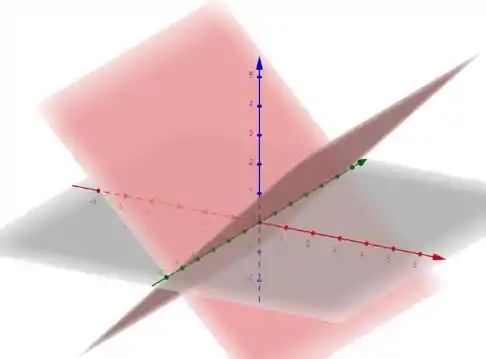
Passo 3
Agora vamos descobrir o que é a nossa superfície :
Pra descobrir isso, precisaremos completar quadrados, já que temos termos quadráticos e lineares na equação, tanto em , quanto em , quanto em .
Vamos lá.
Dividindo os dois lados por :
Temos então três variáveis somadas, elevadas ao quadrado e do outro lado : isso representa um elipsóide deslocado da origem, com centro em .