UTFPR, Sem Campus, Cálculo Diferencial e Integral 2, Listas de Cáclulo 2 - Profº Félix Gómez - Primeira Lista, Questão 1.2d
2] Cada uma das seguintes inequações determina um conjunto de pontos em e . Identificar as bolas abertas e as bolas fechadas identificando o centro e seu raio.
(d)
Passo 1
E aí! Suave na nave?! Tá difícil essa questão? Relaxa que a gente vai te ajudar!
Nesse problema serão dadas inequações de esferas ou círculos e nosso objetivo é identificar o centro e o raio da esfera ou do círculo.
Ok, mas como podemos descobrir isso? 👀
A inequação genérica da esfera é dada por
Onde , e são as coordenadas do centro da esfera e é o raio da esfera.
Já a inequação do círculo é a mesma coisa só que excluindo o termo
Sacou? Bora lá! 😉
Passo 2
A inequação dada é
Como não temos a variável nessa inequação, temos uma estrutura em .
Passando a constante para o outro lado, temos
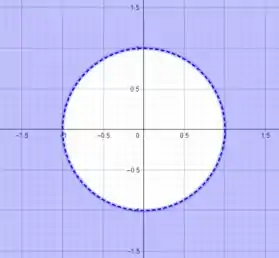
Sabemos que se trata de uma circunferência centrada na origem de raio .
Porém, pelo sinal da inequação, queremos os pontos maiores que , ou seja, os pontos exteriores à circunferência .
O que achou? Foi de boa? Responde aí! 😊
Resposta
Pontos externos à circunferência centrada em e de raio .