UTFPR, Sem Campus, Cálculo Diferencial e Integral 2, Listas de Cáclulo 2 - Profº Félix Gómez - Primeira Lista, Questão 1.1a
1] Representar geometricamente as seguintes bolas
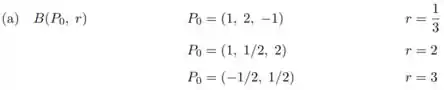
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema queremos obter graficamente as esferas que foram dadas os seus pontos como o centro e seu raio.
Perece de boa, não é? 😁
A equação genérica da esfera é dada por
Onde , e são as coordenadas do centro da esfera e é o raio da esfera.
Sacou? Bora lá! 😉
Passo 2
A primeira esfera é dada por e , ou seja, , , e .
Assim a equação da esfera é dada por
Esboçando essa esfera, temos
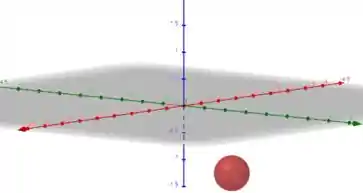
Tranquilo até aqui? 😁
Passo 3
A próxima esfera é dada por e . Assim a equação dessa esfera será dada por
Esboçando essa esfera no espaço...
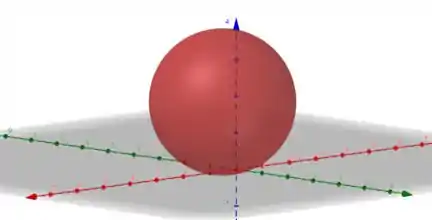
Bacana, não é? 😎
Passo 4
Por fim temos e . Nesse caso não é uma esfera e sim uma circunferência já qua estamos apenas em duas dimensões. Então o que vamos fazer é excluir o termo do nosso problema, ou seja
Esboçando seu gráfico...
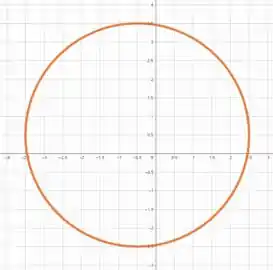
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍