A interseção entre o cilindro , a esfera e o semi espaço é:
- Uma circunferência em um plano paralelo ao plano
- Uma circunferência em um plano paralelo ao plano
- Uma elipse em um plano paralelo ao plano
- Duas elipses, cada uma em um plano paralelo ao plano
- Duas circunferências, cada uma em um plano paralelo ao plano
Passo 1
Vamos tentar pensar essa questão graficamente.
O nosso cilindro
Está ao longo do eixo , pois ele não está aparecendo na equação, logo, pode assumir qualquer valor. E, de fato:
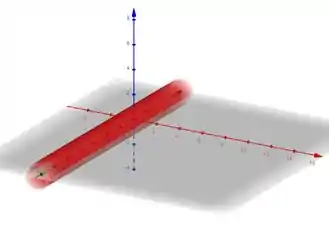
Passo 2
Já a esfera é aquela nossa boa e velha conhecida de sempre:
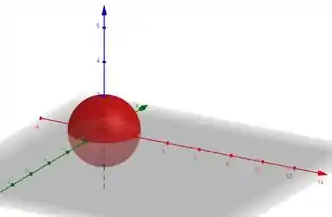
Passo 3
Agora se a gente imaginar o cilindro e a esfera no mesmo desenho, teremos que o nosso cilindro, ao longo do eixo , atravessa a esfera:
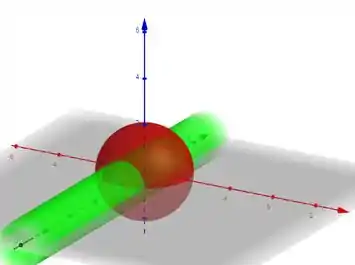
E então ele forma duas circunferências como curva de interseção com a esfera. E essas duas circunferências estão paralelas ao plano .
Então, pimba, letra , certo?
NÃAAAAAAAAO, errado!
A questão diz que tem que fazer interseção com o semi plano . Então a única circunferência que conta para a curva de interseção vai ser aquela que está na parte negativa do eixo .
Assim, a curva de interseção é apenas uma circunferência em um plano paralelo ao plano , sacou?