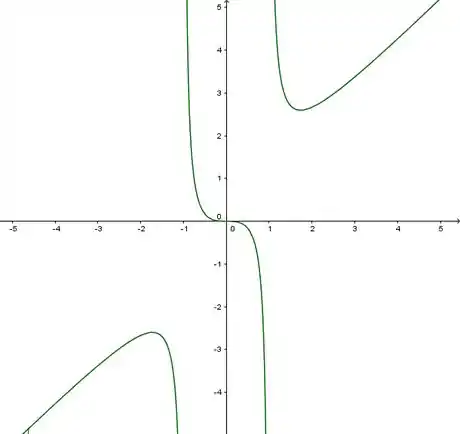
Considere a função dada por
- Determine os intervalos onde cresce, decresce e os pontos de máximo e mínimo locais de .
- Determine os intervalos onde possui concavidade para cima, para baixo e os pontos de inflexão de .
- Calcule os limites pertinentes e discuta a existência de assíntotas.
- Esboce o gráfico de .
Passo 1
(a)
Pra estudar o crescimento da , vamos derivá-la. Pela regra do quociente:
Passo 2
Vejamos quando essa derivada se anula:
Então ou , ou:
Portanto tem pontos críticos: e .
Passo 3
Agora vamos estudar o sinal da derivada, pra determinar onde cresce/decresce, e também classificar esses pontos críticos.
Primeiro, vejamos onde a derivada é positiva:
Para , podemos cortar dos 2 lados da inequação, aí fica:
O que dá no mesmo que:
Passo 4
Agora vejamos onde a derivada é negativa. A conta vai ser praticamente idêntica, só vai mudar o sinal da inequação:
O que vai dar:
Passo 5
Dessa análise do sinal da derivada, tiramos que é crescente no intervalo e decrescente no intervalo .
Logo, pelo teste da primeira derivada, o ponto é um ponto de máximo local, e o ponto é ponto de mínimo local.
Já o ponto não é nem máximo nem mínimo, tadinho. A função decresce em , e também em . A derivada se anulou em , mas não mudou de sinal.
Passo 6
(b)
Nesse item precisamos da segunda derivada. Lembrando que
Pela regra do quociente:
#Eita...ficou bem feia essa segunda derivada. Precisamos dar uma melhorada nela.
Primeiramente, vamos cortar no numerador e no denominador (podemos já que ):
Agora vamos desenvolver esse numerador e simplificar ele:
Ou seja:
Bem melhor né?
Passo 7
Vamos procurar os pontos de inflexão, zerando essa derivada segunda:
Então é o nosso único candidato a ponto de inflexão.
Passo 8
Agora vejamos como varia o sinal dessa derivada segunda. Pra isso vamos montar um quadro de sinais:
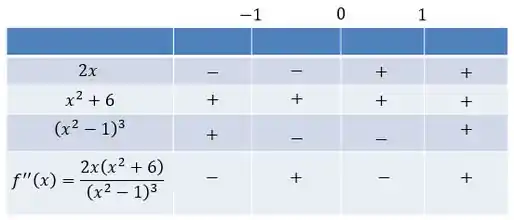
Só uma observação: para , por isso nesse mesmo intervalo temos .
Ok, então a partir do quadro de sinais concluímos que
- tem concavidade para baixo no intervalo
- tem concavidade para cima no intervalo
Repare que a função muda de concavidade em , então esse ponto é de fato um ponto de inflexão.
Com isso matamos a letra (b)! :)
Passo 9
(c)
Agora está declarada a caça às assíntotas. Vamos começar pelas assíntotas verticais, pode ser?
Segundo o próprio enunciado, está definida em todo o menos nos pontos e . Então esses são os nossos candidatos a assíntota vertical.
Vamos calcular os limites laterais da nesses pontos:
Assim confirmamos que e são assíntotas verticais da .
Passo 10
Agora vamos calcular os limites em pra ver se achamos alguma assíntota horizontal.
Mas na hora de calcular
Caímos numa indeterminação “”, então vamos aplicar l’Hôpital pra sair dessa:
Em vai ser praticamente a mesma coisa:
Então nada de assíntota horizontal.
Passo 11
Mas como adoramos assíntotas, vamos averiguar também se o gráfico tem alguma assíntota oblíqua. Se ela existir, o seu coeficiente angular vai ser dado por:
Esses 2 limites têm que existir e ser iguais. Então vamos calculá-los:
Por l’Hôpital, isso dá:
Tá, o limite em deu . Vamos pro limite em :
Da mesma forma, por l’Hôpital, isso dá:
Então o gráfico da tem uma assíntota oblíqua e seu coeficiente angular é .
Passo 12
A equação geral da assíntota oblíqua (que basicamente é uma reta) é:
Achamos , o vamos calcular fazendo:
O que vai dar:
Seja para ou para , caímos numa indeterminação “” e podemos usar l’Hôpital:
Portanto, a equação da assíntota oblíqua é .
Passo 13
(d)
Chegou a hora do esboço. Vamos fazer um breve recapitulativo do (de)crescimento e da concavidade da função:
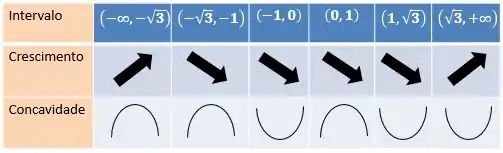
Pra ajudar, podemos também calcular os valores da função em alguns pontos, como os pontos críticos ou de inflexão:
Esses valores não precisam ser muito precisos, eles servem pra ter uma noção na hora do esboço.
Ok, esse foi preciso.
Passo 14
Pensando nisso aí tudo, lembrando também das assíntotas, chegamos enfim no gráfico:
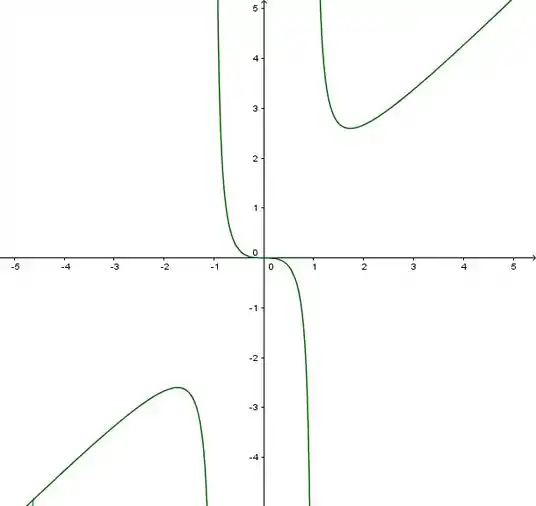
Resposta
(a)
é crescente no intervalo e decrescente no intervalo .
Ponto de máximo local:
Ponto de mínimo local:
(b)
tem concavidade para baixo no intervalo
tem concavidade para cima no intervalo
Ponto de inflexão:
(c)
Assíntotas verticais:
Assíntota oblíqua:
(d)