UFES – Cálculo 1 – Listas de Estudos UFES – Lista 2
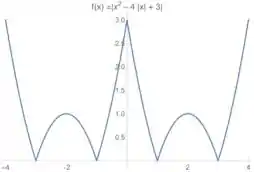
Esboce os gráficos das funções dos exercícios 12. a 17.
17.
Passo 1
Fala aí pessoal, tudo certinho??O problema está nos pedindo para fazer o esboço da função
No fundo ele quer ver como que o gráfico dessa função se comporta, ele não quer nada suuuuper preciso, a gente só precisa marcar a estrutura principal daquele gráfico, ok?A ideia nesse problema é a gente partir de uma função que já conhecemos a cara do gráfico e ir fazendo transformações em cima desse gráfico para a gente obter a cara da nossa função.
OLHA ELA! Ali no meio tem uma função que tem uma cara dessa parábola aqui:
Essa parábola tem concavidade para cima e tem raízes em e em . Ou seja, a gente sabe que o gráfico dessa parábola tem que ter essa cara aqui:
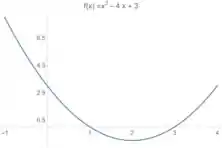
Então vamos lá ver quais tipos de transformações a gente tem que fazer nesse gráfico para ele se tornar a função do nosso problema
Passo 2
A gente vai partir da função
E vai modificando essa função e usando as transformações gráficas que cada transformação implica, beleza?
A primeira coisa que a gente percebe de alteração é que temos ali. Bom essa mudança faz com que a nossa função se torne uma função par:
Certo? E daí??Bom, se a nossa função é uma função par, a gente pode pegar o gráfico de e espelhar a parte da direita do eixo para o lado esquerdo. A gente fica com isso aqui:
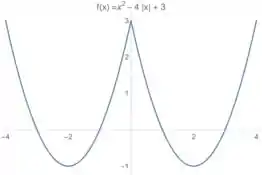
Passo 3
A última coisa que falta é que a gente tem o módulo dessa função que a gente acabou de desenhar o gráfico, certo?
O módulo de uma função , no esboço do gráfico, é pegar as partes que são negativas do gráfico (que estão abaixo do eixo ) e transformá-las em positivas (espelhar para cima do eixo ). Então a gente fica com esse gráfico aqui:
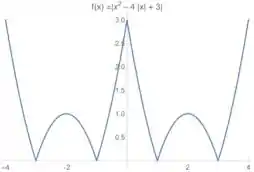
Como ele só quer um esboço, a gente resolveu essa 😊 Vamos para a próxima??
Resposta
