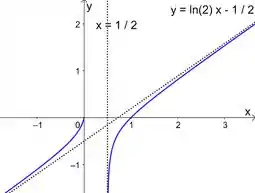
Seja
a) Determine o domínio da função .
b) Determine as equações das retas assíntotas verticais do gráfico de , caso existam.
c) Mostre que a reta é assíntota oblíqua de para a direita (ou seja, quando .
d) Sabendo que é crescente em todo o seu domínio e que a reta é assíntota oblíqua do gráfico de para os dois lados (ou seja, quando e ). Esboce abaixo o gráfico de e suas assíntotas verticais, caso existam.
Passo 1
E aí? Pronta para arrasar nessa questão? Vemo comigo!
Ele pede para determinar o domínio dessa função. Quando a gente vai analisar o domínio, precisamos nos atentar a essas restrições:
E vê se a nossa função tem qualquer uma dessas características, tá bem? Olha, nossa função
Ela tem um denominador: cara percebe que ali no termo , temos um denominador, ele precisa ser diferente de zero, então a gente escreve:
Passo 2
Repara também, que ela tem um log. A gente precisa que esse argumento dele seja estritamente positivo:
Como a gente tem uma fração, vamos precisar estudar o sinal dela para saber em que intervalos ela vai ser positiva.
- : Esse termo zera em
Antes desse ponto ele é negativo e depois é positivo.
- : Esse termo zera em mesmo, antes desse ponto ele é negativo, e depois postivo.
Agora a gente faz a tabelinha para comparar os sinais:
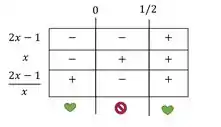
Como nos intervalo e , os sinais de e são iguais, o sinal da divisão entre eles, ou seja, o sinal de vai ser positivo nesses intervalos. Logo, eles são a solução da nossa restrição.
Do outro passo a gente viu que , e isso também aparece aqui já que é aberto em zero, então nosso domínio fica sendo esses dois intervalos que a gente achou aqui:
Passo 3
b) Para achar as assíntotas verticais de
A gente vai calcular os limites laterais nas bordas do seu domínio, aí se explodir para infinito, temos assíntota.
Mas como assim, as bordas? A constantes que limitam o nosso domínio. A gente viu que limita um intervalo pela direita, então a borda que está dentro nosso domínio é
São valores bem próximos de , mas dentro do nosso domínio.
Vimos também que limita nosso domínio pela esquerda. O valores de perto de e dentro do nosso domínio são:
Bora!
Passo 4
Calculando esses limites:
Como dá esse tipo de indeterminação, podemos usar L’Hospital. Repara que a gente vai usar a regra da cadeia:
Já que deu uma constante, não temos assíntota vertical aí, mas nosso gráfico vai tender ao ponto pela esquerda.
Logo, como explodiu para menos infinito, temos que é uma assíntota vertical do nosso gráfico.
Passo 5
c) Precisamos mostrar que a reta é assíntota oblíqua de para a direita (ou seja, quando .
Para fazer isso, vamos tentar montar a equação da reta da assíntota oblíqua de para a direita. Essa equação tem essa cara:
Onde:
Repara que , já que estamos olhando para a direita do gráfico. Bora lá!
Passo 6
Temos
A gente sempre começa calculando :
Agora vamos achar :
Deu uma ideterminação, vamos tentar reescrever isso aí:
A gente pode mexer nisso para dar uma inteterminação do tipo , e com isso poder usar L’Hospital
Aí a nossa reta ficou
Como tínhamos que mostrar!
Passo 7
d) Agora é esboçar o gráfico. Ele diz que é sempre crescente, mas ela só está definida em .
A gente tem a assíntota oblíqua para a direita em e temos a assíntota vertical em .
Esboçando com essas características e a reta , temos esse gráfico lindão:
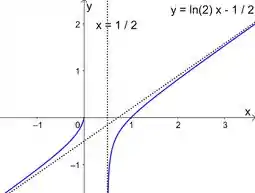
Resposta
a)
b) Só há um assíntota vertical, em
c) Demonstração nos passos 5 e 6
d)