Seja :
Determine todas as assíntotas (verticais, horizontais e oblíquas) justificando quando não houver;
Determine pontos de máximo e mínimo, justificando quando não houver;
Esboce o gráfico de ;
Passo 1
Em primeiro lugar, vou parar para analisar o domínio da função. No caso, como o termo dentro da raiz quadrado será sempre positivo nós vemos que não haverão restrições para o domínio (ou seja, ). As assíntotas que estão ligadas com descontinuidades são as verticais. Se não temos descontinuidades, não teremos assíntotas verticais.
Para determinar as assíntotas horizontais devemos jogar o limite de para e para :
Notamos que não existem assíntotas horizontais também.
Passo 2
Para determinar as assíntotas oblíquas devemos seguir a definição, modelando a reta da assíntota para por e a para por :
Para nós temos que , assim:
Para achamos a assíntota oblíqua .
Passo 3
Fazendo o mesmo raciocínio para modelando a reta por :
Para nós temos que , assim:
Para achamos a assíntota oblíqua .
Passo 4
Vamos analisar a derivada primeira, seu sinal e seus pontos nulos.
Po, esse termo aí tem um denominador que é sempre positivo, correto? Ele está dentro de uma raiz quadrada, então não vai interferir no nosso sinal. Enfim, o sinal de só depende de . Vemos que é positiva para e negativa para . Concluímos que será crescente para e decrescente para havendo um ponto crítico em , com .
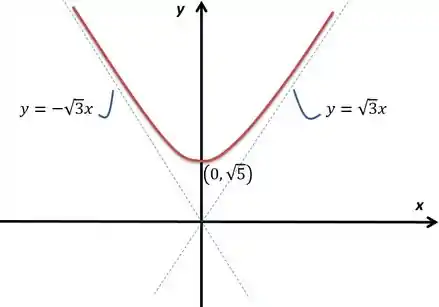
No caso, é um ponto de mínimo, já que a derivada é negativa antes e positiva depois. Agora, esse vai ser um mínimo global, já que a função explode para tanto para quanto para , como vimos no Passo :
A função não possui máximos.
Passo 5
Antes de propriamente fazer o esboço do gráfico devemos fazer a análise da sua derivada segunda, que nos diz informações sobre a concavidade. Vamos calcular a derivada segunda:
Ora, achamos um termo que será sempre positivo, o que nos leva a crer que tem concavidade para cima sempre.
Antes do esboço, uma última informação útil, é uma função par, ou seja, temos que . Resumindo, a função é espelhada em relação ao eixo .