UFES – Cálculo 1 – Listas de Estudos UFES – Lista 2
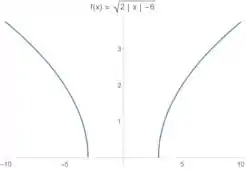
Esboce os gráficos das funções dos exercícios 12. a 17.
13.
Passo 1
Fala aí pessoal, tudo certinho??O problema está nos pedindo para fazer o esboço da função
No fundo ele quer ver como que o gráfico dessa função se comporta, ele não quer nada suuuuper preciso, a gente só precisa marcar a estrutura principal daquele gráfico, ok?A ideia nesse problema é a gente partir de uma função que já conhecemos a cara do gráfico e ir fazendo transformações em cima desse gráfico para a gente obter a cara da nossa função.
A como tem uma raiz ali, a gente vai fazer uso do gráfico de que tem essa cara aqui: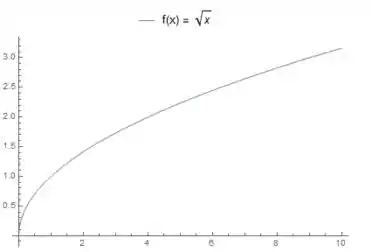
Então vamos lá ver quais tipos de transformações a gente tem que fazer nesse gráfico para ele se tornar a função do nosso problema
Passo 2
A gente vai partir da função
E vai modificando essa função e usando as transformações gráficas que cada transformação implica, beleza?
A primeira coisa que a gente observa é que tem um módulo de ali né ()? Isso significa que a gente pode por valores negativos de também naquela raiz. No fundo, a gente só precisa espelhar esse gráfico em relação ao eixo . Assim ó:
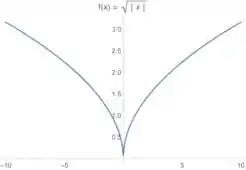
Uma coisa que a gente já pode concluir é que por ter um módulo de ali, a função é par:
Isso implica que tudo que a gente fizer para o lado direita da função, o lado esquerdo vai ser o espelho disso, ok?
Tudo bem até aí, mas o que a gente tem, na verdade, é o que isso implica? Isso só muda os valores de (aumentam um pouquinho):
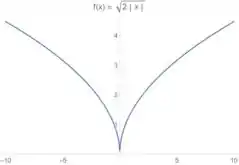
Passo 3
Agora a gente tem que ver como que a gente acrescenta aquele ali. Bom, o que a gente tem é uma transformação do tipo:
E isso corresponde a andar horizontalmente com o gráfico 6 unidades para a direita (vamos pensar só no lado direito do gráfico). Antes de mostrar o gráfico a gente tem que lembrar que tudo que a gente faz no lado direito a gente tem que espelhar para o lado esquerdo, certo?Então a gente vai deslocar o lado direito unidades para a direita e o lado esquerdo unidades para a esquerda. Fica assim ó:
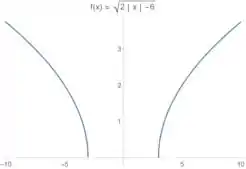
Como ele só quer um esboço, a gente resolveu essa 😊 Vamos para a próxima??
Resposta
