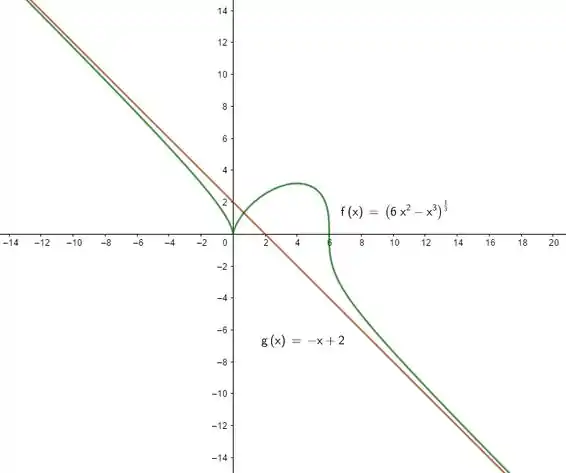
Seja .
- Determine todas as assíntotas (horizontais, verticais e oblíquas) de , justificando quando não houver
- Determine os pontos de máximo e mínimo, justificando quando não houver
- Esboce o gráfico da curva acima
Passo 1
Esse passo vai ser rapidinho, quer ver? Nessa forma, fazer as contas fica complicado! Então vamos desenrolar esse enunciado e escrever . Saca só:
Passo 2
Show, agora que temos , vamos checar as assíntotas verticais. Pra isso, temos que ver o domínio da função. Bom, o domínio vai ser todo o conjunto dos reais menos o conjunto dos pontos que dão problema. Como temos uma raiz cúbica, dentro da raiz podemos ter sim valores negativos!
Se nenhum ponto dá problema, então nenhum é candidato à assíntota vertical e logo não temos assíntotas verticais ;)
Passo 3
Pras horizontais agora, vamos dar uma olhada em como se comporta nos infinitos, beleza? Bora lá:
Como:
E
Vamos ter que
E logo:
Passo 4
Vamos lembrar que as assíntotas oblíquas são definidas por:
Então, uma coisa de cada vez se não a gente se afoba. Primeiro achamos , depois . O cálculo de vai ficar:
Se a gente colocar no numerador o
Agora vamos calcular o valor de . Felizmente só vamos ter pra nos preocuparmos já que também só achamos . Como , calculamos o da seguinte forma:
Puts, esse limite parece complicado. Mas olha um detalhe importante dele: a raiz cúbica! Ela atrapalha, não é mesmo? Que tal tentarmos tirar ela daí usando esse produto notável:
Se fizermos e , multiplicando em cima e em baixo por temos:
Show de bola, numerador simplificado. Agora vamos simplificar o denominador. Vamos abrir o termo :
E colocando em evidência:
Agora, colocando em evidência em , ficamos com:
Jogando isso dentro do denominador:
Colocando em evidência:
E, finalmente, aplicando o limite:
Ufa, cabou! A assíntota oblíqua será então:
Passo 5
Agora vamos ver se a nossa curva tem pontos de máximo ou de mínimo. E pra isso, vamos lembrar do clássico deriva e iguala a zero. Saca só:
Igualando à , temos que:
Ok, mas ainda precisamos ver os pontos em que a derivada não existe. Oras, única forma da derivada não existir é se o denominador for igual à , não é mesmo? Então:
Vamos analisar então o sinal da derivada em intervalos que envolvam esses pontos, ok? Ai sim vamos poder ver quando cresce e quando decresce. Esses intervalos vão ser:
Pro primeiro intervalo, vamos escolher, por exemplo, . Vamos ter:
Pro segundo intervalo, vamos escolher, por exemplo, . Vamos ter:
Pro terceiro intervalo, vamos escolher, por exemplo, . Vamos ter:
E pro último, vamos escolher, por exemplo, . Vamos ter:
Como a função é crescente quando sua primeira derivada é positiva e decrescente quando é negativa, temos que:
Passo 6
É nesse passo que juntamos tudo pra poder esboçar, então vamos lá. Primeiramente, a curva:
Pode ser escrita como uma função:
Dessa curva tiramos as seguintes informações:
- Intercepta o eixo em e
- Intercepta o eixo em
- Não possui assíntotas verticais
- Não possui assíntotas horizontais
- Possui uma única assíntota oblíqua
- Possui os seguintes intervalos de crescimento e decrescimento:
Graficamente, temos:
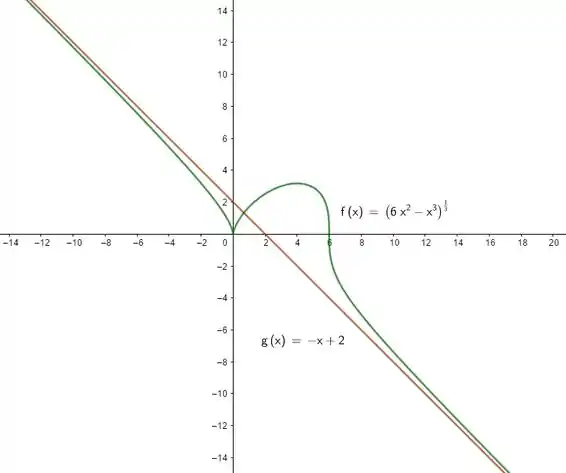
Resposta
- Possui somente assíntota oblíqua:
- Possui pontos de máximo e mínimo em e
- O gráfico da função é dado: