Esboce, no espaço abaixo, o gráfico da função , determinando:
portanto, o gráfico de é:
Passo 1
Vamos juntar tudo que temos:
-
-
-
-
-
-
-
Juntando tudo isso, podemos esboçar a figura:
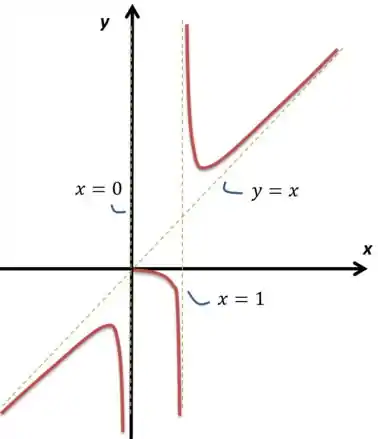
Esboce, no espaço abaixo, o gráfico da função , determinando:
portanto, o gráfico de é:
Vamos juntar tudo que temos:
-
-
-
-
-
-
-
Juntando tudo isso, podemos esboçar a figura:
