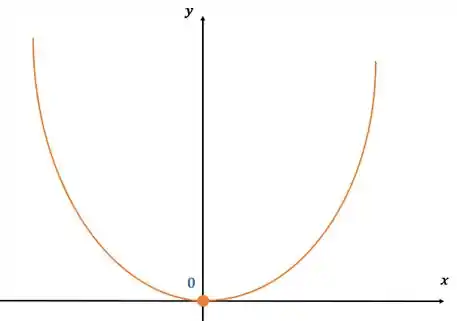
Para a próxima função:
- Encontre os intervalos para os quais a função é crescente ou decrescente;
- Encontre os valores de máximo e mínimo locais;
- Encontre os intervalos de concavidade e os pontos de inflexão;
- Encontre as assíntotas horizontais e verticais;
- Esboce o gráfico, utilizando as informações dos itens anteriores.
Passo 1
Galerinha, essa é mais uma questão de montar gráfico e para chegar nesse final triunfante, iremos passar por cada um dos itens que ele nos pede no enunciado. Então vamos começar pela função:
Sobre o crescimento e decrescimento, como fazemos isso? Regra da Primeira Derivada!
Então vamos derivar essa função utilizando a Regra do Produto:
Fazendo essas derivadas dentro da nossa expressão:
Logo a primeira derivada pode ser reescrita como:
Agora precisamos encontrar quais valores onde nossa primeira derivada é igual a zero dentro do nosso intervalo! Vamos relembrar nosso intervalo:
Para isso, o numerador deveria ser igual a zero:
Temos que ter duas parcelas iguais a zero, tanto a tangente:
Quanto o produto:
A tangente é igual a zero em dois pontos:
Como nosso intervalo é:
Então a única opção é:
E isso faz o produto também ser igual a zero:
Então nossa derivada será:
Vamos colocar todos os elementos em nosso quadro de sinais:
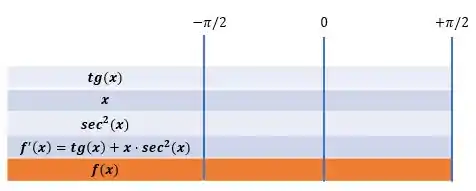
A tangente assumirá valores positivos para o intervalo de , enquanto assume valores negativos para o intervalo :
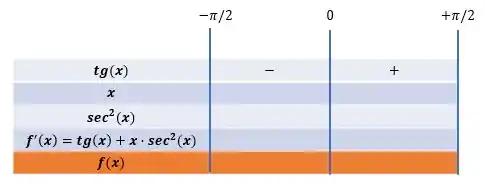
Por outro lado, o valor da secante elevado ao quadrado sempre será positivo, exatamente por estar elevado ao quadrado:
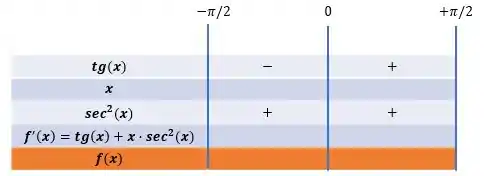
Enquanto a expressão de assume o sinal positivo caso esteja acima do valor zero e assume sinal negativo caso, o intervalo seja inferior a zero:
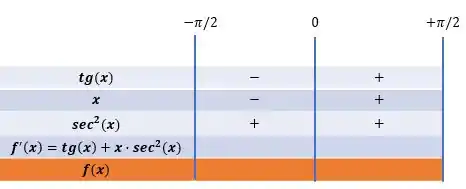
Dessa forma, o produto entre os fatores do numerador e a divisão deste pelo denominador resulta nos sinais da primeira derivada nos intervalos:
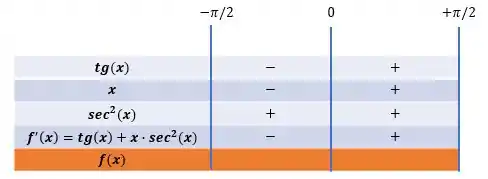
E o que sabemos através da Regra da Primeira Derivada:
- Se , então é crescente nesse intervalo;
- Se , então é decrescente nesse intervalo.
Baseado nessa regra, podemos assumir que a função terá o seguinte comportamento:
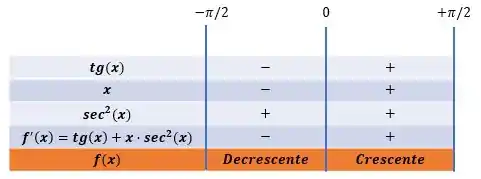
é crescente no intervalo:
é decrescente no intervalo:
Passo 2
Já achamos a primeira resposta, hora de olha para o segundo pedido de nossa questão, na letra “b”, o enunciado nos diz para encontrar os valores de máximo e mínimo locais. Para isso, vamos usar um pouco do que já construímos no item anterior!
Quando ocorre o ponto de máximo ou ponto de mínimo? Bom, isso ocorre quando a derivada primeira de uma função é igual a zero!
No último passo, descobrimos que isso ocorre nos pontos:
Analisando que antes de temos um decrescimento e após esse ponto a função começa a crescer, então:
Passo 3
Na letra “c”, o enunciado nos pede para encontrar os pontos de inflexão e a concavidade que a função assume. E como começamos isso? Teste da Segunda Derivada!
Se a nossa primeira derivada vale:
Para encontrar a segunda derivada, vamos separar em duas derivadas:
Nossa segunda parte é:
Resolvendo essa Regra do Produto:
Vamos voltar a nossa Segunda Derivada:
Podemos então simplificar da forma:
Colocando em evidência:
Olha, pessoal, nos baseando no quadrinho do primeiro passo, nós sabemos que o produto:
É sempre maior que zero em nosso intervalo . E como sabemos que a secante elevada ao quadrado é sempre maior que zero, então TODA a nossa segunda derivada é maior que zero!
Pela Regra da Segunda Derivada, temos:
- Se , então tem concavidade para cima nesse intervalo;
- Se , então tem concavidade para baixo nesse intervalo.
- Intervalos de Crescimento e Decrescimento:
- Pontos de Máximo e Mínimo:
- Concavidade:
- Assíntotas:
Logo em todo o nosso intervalo, a concavidade da função é para cima!
Não existem pontos de inflexão! Pois percebemos que em nenhum ponto a segunda derivada é igual a zero!
Passo 4
A letra “d” é: Encontre as assíntotas horizontais e verticais.
Começando pela assíntota horizontal:
Se substituirmos o valor de :
Como a tangente de tende ao infinito, então:
Não encontramos uma assíntota horizontal!
Partindo para o outro lado :
Quando aproximamos o valor de por números maiores que o valor da tangente se aproxima de infinito negativo, então:
Não encontramos uma assíntota horizontal!
Partindo para assíntotas verticais, vamos ver onde temos uma descontinuidade! No caso da nossa função:
No intervalo:
Nesse intervalo não existe descontinuidade! Logo, não existe assíntota vertical!
Passo 5
E por último, vamos esboçar esse gráfico, nos baseando em todas as informações que nós levantamos anteriormente.
é crescente no intervalo:
é decrescente no intervalo:
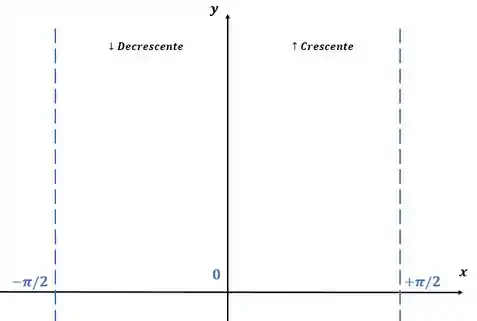
Marcando esses pontos:
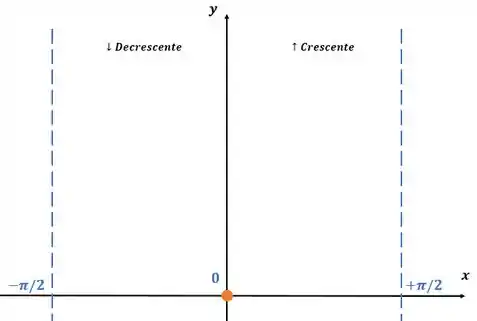
Não existem pontos de inflexão!
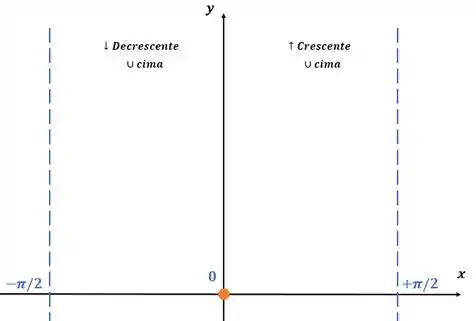
Porém sabemos que quando nos aproximamos dos pontos extremos do intervalo, temos:
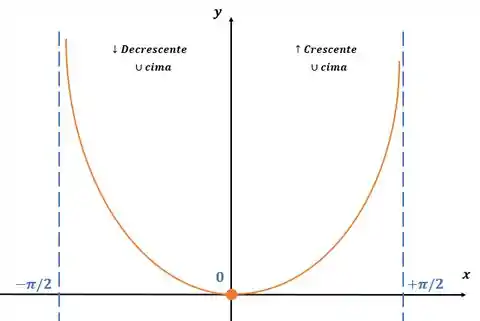
Ficamos então com o gráfico:
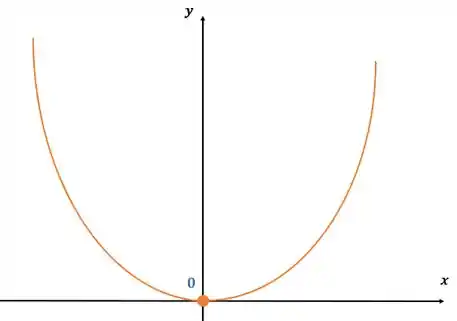
Resposta
-
é crescente no intervalo:
é decrescente no intervalo:
-
Não existem pontos de inflexão!