Considere a função
Determine, caso existam:
a) as equações das assíntotas horizontais do gráfico de .
b) as equações das assíntotas oblíquas do gráfico de .
c) os intervalos de crescimento e de decrescimento de .
d) Utilizando as informações obtidas nos itens anteriores, esboce o gráfico da função e suas retas assíntotas. Mas em seu desenho as abcissas dos pontos de máximo local e mínimo local do gráfico de , caso existam.
Passo 1
a) Vamos lá! Para achar as assíntotas horizontais de
a gente vai calcular os limites dessa função quando 𝑥→∞ e 𝑥→−∞. Aí se eles derem um número, sabemos que temos esse tipo de assíntota, belezinha?
Vamos começar olhando se há uma assíntota na direita do gráfico:
Como a gente caiu numa indeterminação do tipo , podemos usar L’Hospital:
Vamos usar L’Hospital de novo:
Como deu um número, a gente pode dizer que há uma assíntota para a direita de equação .
Passo 2
Vamos ver se tem assíntota para a esquerda:
Daí a gente tira que não temos assíntota para a esquerda, já que nosso limite explodiu para infinito, ou seja, não deu um número.
Passo 3
b) Precisamos achar as assíntotas oblíquas. Só teremos duas no máximo, uma para esquerda e outra para direita. Maaas, como a gente já tem uma assíntota horizontal para a direita, não teremos a oblíqua para esse lado.
Então a gente só precisa testar se há uma assíntota oblíqua para a esquerda. E para fazer isso, a gente vai tentar montar a equação da reta que representa essa assíntota:
Calculando os limites:
Repara que , já que estamos olhando para a esquerda do gráfico. Bora lá!
Passo 4
Temos
A gente sempre começa calculando :
Como esse explodiu para menos infinito, a gente vai dizer que não há assíntotas oblíquas no nosso gráfico.
Passo 5
c) Determinar os intervalos de crescimento e decrescimento de uma função é o mesmo que ver os intervalos onde a derivada assume valores positivos (aí a função está crescendo) e valores negativos (aí nossa função está decrescendo).
Bora começar derivando a função:
Como é uma fração, precisamos usar a regrinha do quociente:
Passo 6
A gente vê que o termo não vai influenciar no nosso sinal, porque ele é sempre positivo e está em produto com o outro termo. Aí podemos olhar só para o sinal do termo que sobrou:
Vamos achar em que pontos ele zera (porque aí encontramos os intervalos onde os sinais são diferentes entre si).
Então a gente precisa avaliar o sinal da derivada nesses intervalos:
Passo 7
Vamos testar o sinal da derivada em cada um deles:
-
Podemos escolher um ponto dentro desse intervalo para ver o sinal da derivada, por exemplo :
Como deu um valor negativo, a gente diz que nossa função está decrescendo nesse intervalo.
-
Podemos escolher um ponto dentro desse intervalo para ver o sinal da derivada, por exemplo :
Como deu um valor positivo, a gente diz que nossa função está crescendo nesse intervalo.
-
Podemos escolher um ponto dentro desse intervalo para ver o sinal da derivada, por exemplo :
Como deu um valor negativo, a gente diz que nossa função está decrescendo nesse intervalo.
Passo 8
d) Agora chegou o momento de usarmos tudo o que a gente achou para esboçar esse gráfico.
E ele pede também para marcar as abscissas dos pontos de máximo e mínimo. Esses são os pontos críticos da nossa função. Pontos onde a derivada zera. Vimos que ela zera em:
Vamos marcar eles!
Aí respeitando os intervalos de crescimente e decrescimento que a gente achou, e colocando só uma assíntota na direita em , nosso gráfico fica assim:
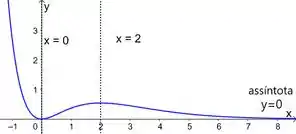
Resposta
a) , só há uma assíntota para a direita
b) não há há assíntotas oblíquas
c) Intervalos de decrescimento:
Intervalo de crescimento:
d)