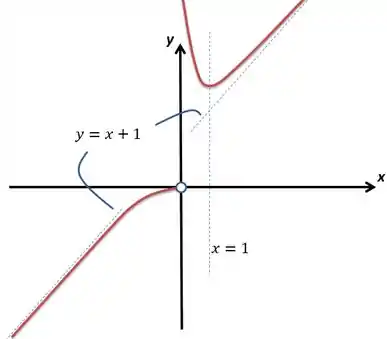
Considere a função :
Determine o domínio de .
Determine os pontos de máximo e mínimo locais de .
Determine todas as assíntotas da curva .
Esboce o gráfico de contemplando todos os elementos obtidos acima.
Passo 1
No termo da função só temos um limitante para nosso domínio: o do expoente não pode ter seu denominador nulo, ou seja, temos que ter .
Passo 2
Para procurar máximos e mínimos devemos otimizar a função, derivando ela e igualando a zero para achar os pontos críticos. Vamos derivar pela Regra do Produto:
O único ponto onde é quando , nosso único ponto crítico.
Se não faz parte do domínio nós vemos que essa derivada é contínua em todo domínio. O sinal não depende da exponencial, então só dependerá do e do . Vamos fazer o quadro de sinais para esses termos, assim podemos analisar se o ponto é de máximo ou de mínimo em :
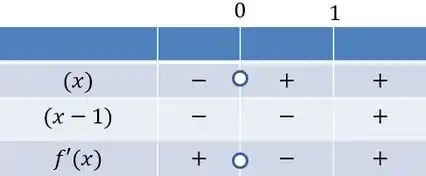
Como vemos, a derivada é negativa entre e e a partir daí é positiva, o que constitui um ponto de mínimo. Vemos também que a função é crescente em e , sendo decrescente em .
Passo 3
Procuramos por assíntotas. Sabemos que as verticais estão relacionadas com descontinuidades no domínio. Sendo assim, vamos ver se algum dos limites laterais na descontinuidade explode para :
O limite lateral por valores maiores que explodiu para , assim a gente já garante que tem uma assíntota vertical em .
Passo 4
Vamos olhar agora por assíntotas horizontais:
Não existem assíntotas horizontais, já que os limites explodiram para , mas ainda podem haver assíntotas oblíquas!
Passo 5
Vamos modelar as assíntotas por para o lado do e por para . Por definição, os coeficientes das assíntotas são dados por:
Achamos a assíntota para a direita. Agora procuremos para a esquerda, com tendendo a .
A mesma assíntota, achamos para a esquerda.
Passo 6
Agora partiríamos para o esboço. Antes vamos fazer a análise da derivada segunda, que nos dá informações sobre a concavidade do gráfico. Achamos a derivada segunda pelas Regras de derivação do Produto e do Quociente:
Como vemos, se a exponencial é um valor sempre positivo, vemos que o sinal da derivada segunda só depende de , que é negativo em e positivo para . Resumindo, concavidade para cima para valores positivos e para baixo para valores negativos.
Agora, juntando tudo que vimos na questão, temos o seguinte:
Assim, o gráfico será: