Seja . Determine o que se pede justificando a não existência, se for o caso:
- Domínio
- Ponto de interseção do gráfico da função com os eixos cartesianos
- Intervalo de crescimento e decrescimento
- Máximos e mínimos locais
- Assíntotas horizontais, verticais e oblíquas
- Desenhe o gráfico de com todos os elementos encontrados acima
Passo 1
Primeiro vamos ver o domínio, temos dois detalhes com problemas ali, o cara dentro do logaritmo e a raiz quadrada, primeiro esse cara dentro do log precisa ser positivo, ou seja:
Mas como raiz quadrada é algo sempre positivo isso está certinho.
O outro problema é que o cara dentro da raiz deve ser positivo, repara que eu ignoro quando a raiz for por causa do log:
Então qualquer valor de nesse intervalo, o cara dentro da raiz é maior que e o cara dentro do log tbm, então o domínio são os reais:
Passo 2
Para achar os pontos de interseção com os eixos coordenados basta fazer a função quando e achar o e depois fazer e achar o .
Vamos começar fazendo :
E a parada fica por isso mesmo, o ponto que ele corta o eixo é .
Vamos ver agora com :
Usando propriedades de log vamos ter:
O ponto que ele corda o eixo vai ser .
Passo 3
Para olhar o intervalo de crescimento vamos olhar a derivada, vamos derivar a função:
Temos um log meio louco ali no meio, normalmente derivamos só o logaritmo na base , vamos usar propriedades de logaritmo e fazer essa mudança de base:
Vamos ter:
Essa derivada só depende do sinal de , mas no domínio vai ser sempre positivo, lembra que ele precisa ser positivo para a raiz não dar problema? Isso nos diz que:
Em todo o domínio, ou seja, é sempre crescente.
Passo 4
Como a função é sempre crescente ela não vai ter nenhum extremo em todo o domínio.
Passo 5
A primeira pergunta é WTF é assíntota inclinada, fuuuuuuuuu!!!!

Relaxa, vamos primeiro para a assíntota que você conhece, a assíntota horizontal, como eu acho a assíntota horizontal?
Temos que fazer:
Dessa vez não fazemos isso porque o domínio começa no e não “começa” no .
Vamos começar com o limite para .
Logo ele não vai ter assíntotas horizontais.
Passo 6
Vamos entender a assíntota inclinada, isso vai ser uma reta inclinada que a função se aproxima, a questão está em como calcular a reta.
Uma reta inclinada, vai ser assim:
Precisamos achar os coeficientes e da assíntota obliqua, podemos ter dois pares de coeficientes, um vai ser o par de baixo:
Beleza? Não fazemos o pelo mesmo motivo da horizontal, vamos achar o valor de :
Já vimos que a parte de cima vai dar então isso vai dar uma indeterminação , vamos aplicar L’Hôpital:
Já temos a derivada de né? Então vai ficar
Precisaríamos ter , mas uma reta assim não é inclinada, então não vamos ter assíntota oblíqua.
Passo 7
Vamos ver agora a assíntota vertical, aqui o único cara que nos interessa é quando o que está dentro do log for , então vamos pegar o limite quando
Eu coloquei pela direita porque o nosso domínio só tem a parte maior que
Então como o limite vai para temos uma assíntota vertical que vai ser
Passo 8
O esboço do gráfico vai ficar:
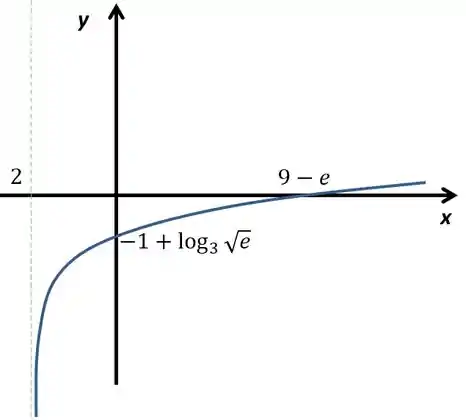
Resposta
- O ponto que ele corta o eixo é
- É crescente em todo o domínio
- Não possui máximo e mínimos
- Não tem assíntotas horizontais ou oblíquas
O ponto que ele corda o eixo vai ser
Assíntotas verticais: