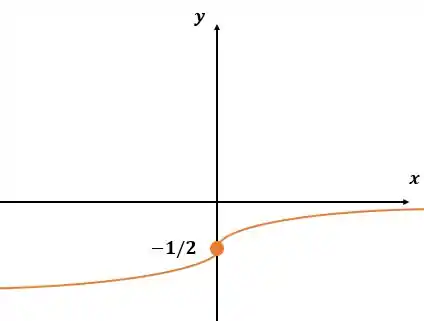
Para a próxima função:
- Encontre os intervalos para os quais a função é crescente ou decrescente;
- Encontre os valores de máximo e mínimo locais;
- Encontre os intervalos de concavidade e os pontos de inflexão;
- Encontre as assíntotas horizontais e verticais;
- Esboce o gráfico, utilizando as informações dos itens anteriores.
Passo 1
Fala aí, amigão! Temos um passo a passo que vai nos ajudar a construir no final o nosso gráfico, beleza? Então mãos a obra!
Nossa função é:
Nosso primeiro passo é encontrar os intervalos para os quais essa função é crescente e quais ela é decrescente. E como fazemos isso? Se você respondeu Regra da Primeira Derivada, você ACERTOU!
Então vamos derivar essa função :
Logo a primeira derivada pode ser reescrita como:
Agora precisamos encontrar quais valores onde nossa primeira derivada é igual a zero! Você pode perceber que esse valor não existe independentemente do valor de ! Logo, não temos ponto de mínimo nem de máximo!
Além disso, vamos encontrar o valor para o qual a primeira derivada não existe. Olhando a nossa primeira derivada:
Ela não existe, caso o denominador seja igual a zero, mas o denominador é sempre maior que zero:
Como tanto o numerador quanto o denominador são maiores que zero, então, nossa primeira derivada é sempre positiva!
E o que sabemos através da Regra da Primeira Derivada:
- Se , então é crescente nesse intervalo;
- Se , então é decrescente nesse intervalo.
Como a primeira derivada é sempre maior que zero, então a função é sempre crescente!
é crescente no intervalo:
Passo 2
Já achamos a primeira resposta, hora de olha para o segundo pedido de nossa questão, na letra “b”, o enunciado nos diz para encontrar os valores de máximo e mínimo locais. Para isso, vamos usar um pouco do que já construímos no item anterior!
Quando ocorre o ponto de máximo ou ponto de mínimo? Bom, isso ocorre quando a derivada primeira de uma função é igual a zero!
No último passo, descobrimos que isso não ocorre em nenhum ponto dentro do domínio da função, logo, não existe ponto de máximo ou de mínimo local!
Passo 3
Na letra “c”, o enunciado nos pede para encontrar os pontos de inflexão e a concavidade que a função assume. E como começamos isso? Teste da Segunda Derivada!
Se a nossa primeira derivada vale:
Para encontrar a segunda derivada, vamos usar a Regra do Quociente:
Reescrevendo os produtos:
Colocando em evidência:
Temos a diferença entre dois quadrados, então podemos reescrever a partir do produto notável:
Pela Regra da Segunda Derivada, temos:
- Se , então tem concavidade para cima nesse intervalo;
- Se , então tem concavidade para baixo nesse intervalo.
- Intervalos de Crescimento e Decrescimento:
- Pontos de Mínimo:
- Concavidade:
- Assíntotas Horizontais:
O numerador é igual a zero quando:
Como é sempre positivo, logo a única forma desse numerador ser igual a zero é se:
Isso ocorre se:
Vamos montar um quadrinho de sinais:
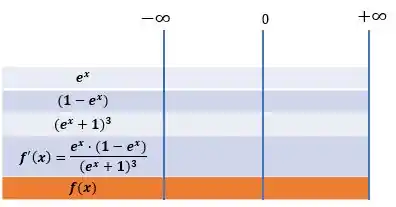
A função sempre assume valores positivos para qualquer valor de :
A função é maior que , quando . Dessa forma:
Dessa forma, para valores de maiores que , então a função assume valores negativos:
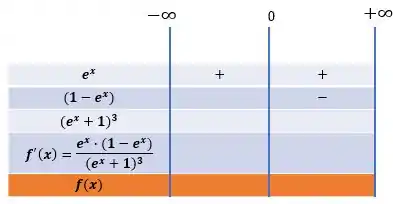
Para valores de menores que , a função assume valores positivos:
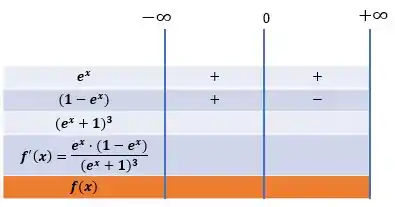
Por outro lado, se a função é maior que zero, o denominador é sempre positivo:
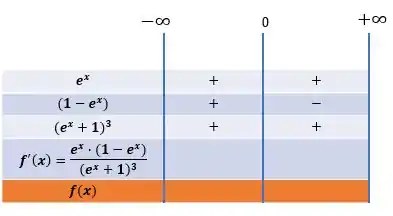
Dessa forma, realizando o produto entre os elementos do numerador e dividindo pelo elemento do denominador, a segunda derivada terá como sinal:
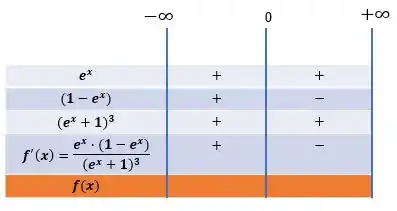
Como já falamos sobre as regras da segunda derivada, as concavidades serão determinadas pelo sinal de cada intervalo:
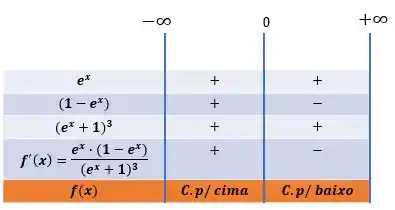
Ponto de inflexão:
Passo 4
A letra “d” é: Encontre as assíntotas horizontais e verticais e inclinadas.
Começando pela assíntota horizontal:
Se substituirmos o valor de :
Encontramos uma assíntota horizontal!
Partindo para o outro lado :
Temos outra assíntota horizontal!
Partindo para assíntotas verticais, vamos ver onde temos uma descontinuidade! No caso da nossa função:
Como já falamos que a função é sempre maior do que zero:
Logo, não temos descontinuidade dessa função e portanto, não existe assíntota vertical!
Como existem assíntotas horizontais, sabemos quem não existem assíntotas inclinadas, também chamadas de assíntotas oblíquas.
Passo 5
E por último, vamos esboçar esse gráfico, nos baseando em todas as informações que nós levantamos anteriormente.
é crescente no intervalo:
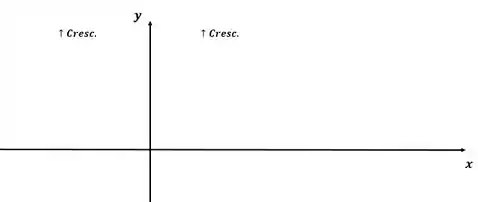
Ponto de inflexão:

Vamos marcar o ponto de inflexão:
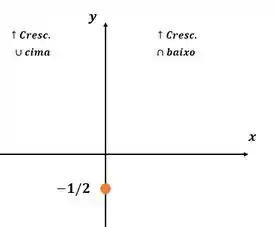
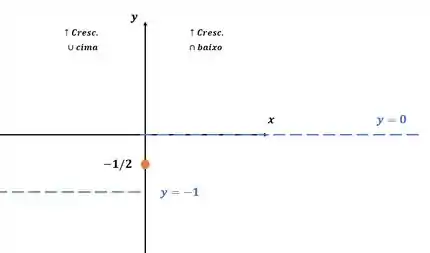
Ligando os pontos:
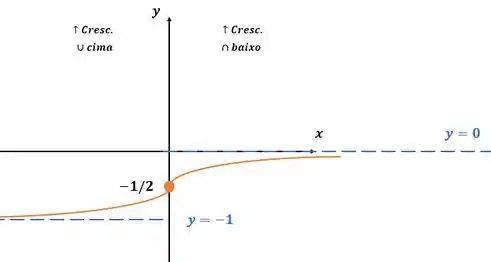
Resposta
-
é crescente no intervalo:
-
Ponto de inflexão:
-
Assíntotas Horizontais: