Seja .
- Determine todas as assíntotas (horizontais, verticais e oblíquas) de , justificando quando não houver
- Determine os pontos de máximo e mínimo, justificando quando não houver
- Esboce o gráfico da curva acima
Passo 1
Vamos começar vendo se essa função tem assíntotas verticais, beleza? Pra ter assíntota horizontal, tem que ter algum ponto “que dê problema”, ou seja, alguma forma de gerarmos uma indeterminação.
Como nosso tem uma parcela , não vai ser qualquer que eu escolha que vai estar tudo bem! Logo, , um valor que gera indeterminação, é um candidato à assíntota vertical! Então partiu descobrir se ele é mesmo fazendo os limites:
Opa, como os limites são pro infinito, é sim uma assíntota vertical!
Passo 2
Agora, pras horizontais, vamos fazer quando tende aos infinitos. Se a gente receber um número como resposta é porque a função tende a esse valor, mas nunca chega lá, beleza? Ai sim teremos assíntotas. Então, fazemos:
Escrevendo dessa forma a gente pode usar o famoso L’Hospital! Pra , temos:
Pra , temos:
E já que os limites aqui foram ao infinito, não vamos ter assíntotas horizontais, beleza? Partiu agora as próximas assíntotas:
Passo 3
Vamos lembrar que as assíntotas oblíquas são definidas por:
Então, uma coisa de cada vez se não a gente se afoba. Primeiro achamos , depois . Para a função , o cálculo de vai ficar:
Opa, nem precisamos fazer dois limites diferentes, pra + e - , porque o limite que sobrou vai direto pra !. Beleeeeza, a inclinação da assíntota oblíqua vai ser então:
E pra calcular , fazemos:
Fechamos então a equação oda assíntota oblíqua, que vai ser:
Passo 4
Agora vamos tentar achar pontos de máximo e de mínimo, beleza? Pra isso temos que fazer o clássico deriva e iguala a . Então vamos lá:
Igualando à agora:
Então temos pontos críticos! Vamos checar o sinal da derivada em intervalos que envolvam esses pontos, ok? Mas também não podemos esquecer do ponto , que é um ponto em que nossa primeira derivada não está definida. Intervalos que envolvam esses valores de vão ser:
Pro primeiro intervalo vamos escolher, por exemplo, . Vamos ter:
Pro segundo intervalo vamos escolher, por exemplo, . Vamos ter:
Pro terceiro intervalo vamos escolher, por exemplo, . Vamos ter:
Pro quarto intervalo vamos escolher, por exemplo, . Vamos ter:
Como a função é crescente quando a primeira derivada é positiva e decrescente quando ela é negativa, os intervalos de crescimento e decrescimento vão ser:
Como primeiro cresce e depois decresce, o ponto vai ser então um ponto de máximo local e como decresce e depois cresce, o ponto vai ser então um ponto de mínimo local
Passo 5
Agora vamos juntar todas as informações que temos para esboçar o gráfico. Temos que:
- A função possui uma única assíntota vertical
- A função não possui assíntotas horizontais
- A função possui somente uma assíntota oblíqua
- é um ponto de máximo local
- é um ponto de mínimo local
Juntando isso tudo, esboçamos o gráfico:
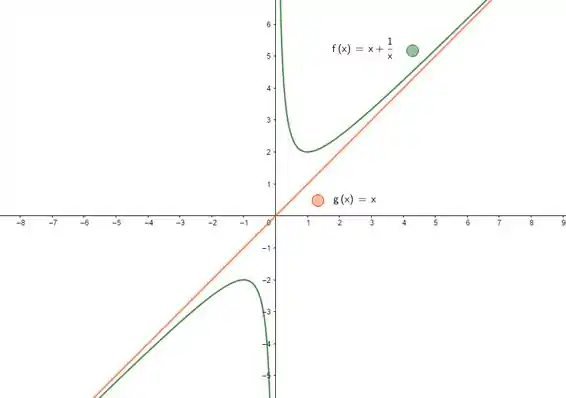
Resposta
- Não possui assíntotas horizontais, mas possui uma assíntota vertical em e uma oblíqua
- Possui pontos de máximo e de mínimo locais, respectivamente em e
- O gráfico é dado: