Questão 2:

Considere a função definida por

1. Determine o domínio da função .
2. Determine os intervalos de crescimento e os de decrescimento de , caso existam.
3. Determine as equações das retas assíntotas horizontais do gráfico de , caso existam.
4. Determine as equações das retas assíntotas verticais do gráfico de , caso existam.
5. Determine as equações das retas assíntotas oblíquas do gráfico de , caso existam.
6. Sabendo que no intervalo o gráfico de tem concavidade voltada para baixo, e que no intervalo o gráfico de tem concavidade voltada para cima, utilize as informações obtidas nos itens anteriores para esboçar o gráfico de e suas retas assíntotas, caso existam.

Para determinar os intervalos de crescimento ou decrescimento sempre devemos analisar o sinal da primeira derivada, pois...

Então calculemos a primeira derivada...

Aplicando a regra do produto...

Calculando essa outra aplicando a regra da cadeia...

Bem, a função potencial é sempre positiva, então o sinal da derivada depende inteiramente do termo...

Vamos analisar o ...

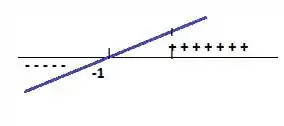
Enquanto o ...

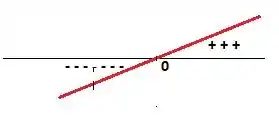
Logo, a divisão...

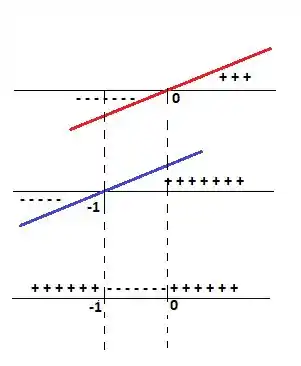
Como o sinal da primeira derivada depende inteiramente desse sinal, podemos afirmar que...

Logo, a função é crescente em...

E decrescente no intervalo...

Para buscar as assíntotas horizontais, calculemos o limite da função quando ela vai para os infinitos...

Para o primeiro limite...

Repare que quando vai ao infinito, o expoente vai a enquanto então a exponencial vai a , enquanto que o vai ao infinito...

Já o outro limite...

A exponencial continua indo a , mas o vai ao infinito negativo, logo...

Então não existe assíntotas horizontais ;)

Para as assíntotas verticais, também calculemos limites, mas dessa vez, ao invés de um limite no infinito, calculemos o limite próximo do ponto problemático que não está no domínio:

Se os limites:

Forem infinitos, então o é uma e única assíntota vertical. Única porque não tem outros pontos de problema no domínio, saca?

Então vamos lá!

Quando o vai a pelos positivos, temos algo do tipo...

Sacou? Pois os dois vão a , logo produto também vai!

Agora...

Epa! Agora a coisa muda de figura, pois quando tendemos a pelos negativos é positivo e tende ao infinito, logo, ganhamos uma indeterminação do tipo: ...

E importante, esse limite não é . Essa é uma indeterminação que para resolver, perceba que podemos fazer L’Hopital caso conseguimos um ...

Prontinho! Agora é só aplicar o Teorema...

Aplicando a regra da cadeia no nominador...

Já vimos que esse cara está indo para o infinito positivo, logo...

Como um dos limites laterais foi ,

Isso significa que sim, é uma assíntota vertical

Não morra de tédio, ainda faltam às assíntotas oblíquas. Uma assíntota oblíqua tem equação...

Onde o , pode ser encontrado (se tiver assíntota obliqua) fazendo...

Como a exponencial se aproxima de , pois o expoente vai a ...

Então existe assíntota oblíqua. Para encontrar o ...

Repare que agora existe uma indeterminação, pois o termo do vai ao infinito enquanto que o termo do parênteses vai a , então temos uma indeterminação do tipo . Aplicando L’Hopital...

Então uma assíntota oblíqua é ...

Mas calma, ainda não acabou esse item, pois pode ter outra assíntota quando o vai ao infinito, mas dessa vez negativo:

Onde

Então .

Como já simplificado por L’Hopital no passo anterior...

Logo, para o lado negativo, a assíntota oblíqua é a mesma:

Bem, colocando todas as informações juntas:

• A função não está definida no , embora quando nos aproximamos de pela direita é e pela esquerda é uma assíntota vertical .
• Além disso, sabemos que ela tem esse aspecto com relação ao crescimento e as concavidades:

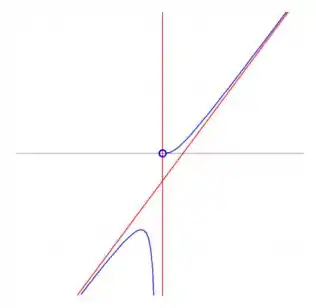
Logo a curva só pode ser algo assim:

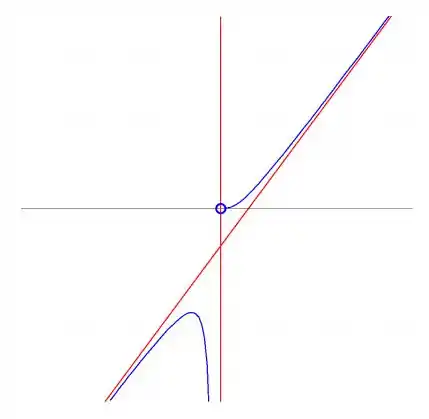
Essa linha vermelha é a assíntota oblíqua dela !

Ufa! Enfim...