UFES – Cálculo 1 – Listas de Estudos UFES – Lista 2
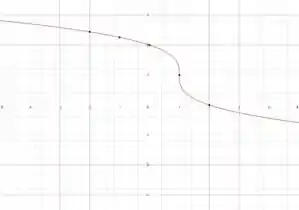
Esboce os gráficos das funções dos exercícios 12. a 17.
15.
Passo 1
Fala aí pessoal, tudo certinho??O problema está nos pedindo para fazer o esboço da função
No fundo ele quer ver como que o gráfico dessa função se comporta, ele não quer nada suuuuper preciso, a gente só precisa marcar a estrutura principal daquele gráfico, ok?
Por conta daquela raiz cúbica a gente vai ter que mudar um pouco a forma com que a gente vê essas equações. O que vai nos ajudar nesse problema é pensar em como sendo e escrever como uma função de
A função que vai aparecer em a gente já vai ter uma ideia do seu comportamento. Aí no fundo é só deitar essa função de lado que vai ser a nossa resposta!
Parece um papo meio doido mas vem comigo que a gente vai entender a razão disso!
Passo 2
Primeiro vamos fazer essa história de escrever como função de A gente faz isso, chamando de e manipulamos um pouco aquela expressão para termos isso aqui:
Elevando ao cubo os dois lados temos:Isolando :Opaaa! A gente conhece a cara de uma função cúbica:
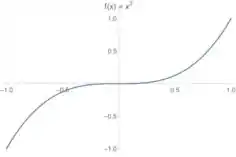
Só que essa daí é em função de . Para termos em função de a gente só precisa deitar essa curva e espelhar verticalmente. Vou fazer isso com essa imagem aqui de cima só para vocês terem uma ideia do que acontece:
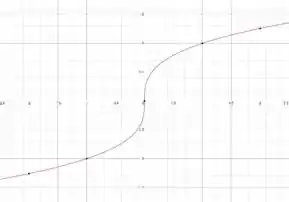
O que a gente vai fazer agora é partir desse gráfico e fazer as transformações tomando cuidado que a variável em questão agora é . Beleza??
Passo 3
A primeira coisa que a gente pode perceber é que não temos apenas ali, temos então vamos buscar o gráfico de primeiro. Para esse gráfico a gente observa que partindo de temos uma transformação do tipo:
Isso corresponde a andar verticalmente com o gráfico (aquele de que a gente conhece) unidade para cima. Fica assim ó:
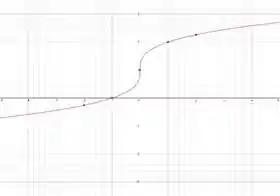
Passo 4
Outra coisa que a gente observa é que não temos temos . Trocar o sinal dessas duas funções corresponde a espelhar em relação ao eixo esse gráfico. Então a gente fica com isso aqui:
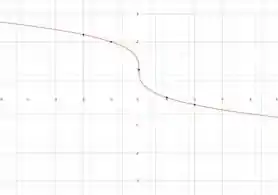
Estamos quase lá!!
Passo 5
Por fim, a gente tem que adicionar nessa função que a gente mexeu até agora, né?
Que corresponde a andar horizontalmente com esse gráfico unidade para a direita:
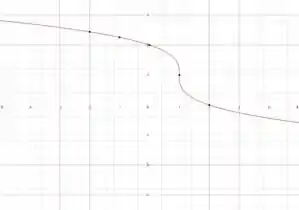
Como ele só quer um esboço, a gente resolveu essa 😊 Vamos para a próxima??
Resposta
