Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Esboço de Gráfico – Assíntota Oblíqua

Ver Teoria
Exercício 712345689101112131415161718192021222324252627282930313233343536373839

Enunciado

Esboço de Curvas

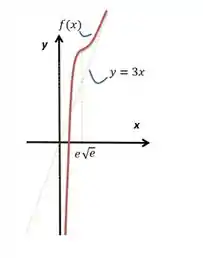
b ) Esboce o gráfico de f x = 3 x + ln ⁡ x x , determinando seu domínio, os intervalos de crescimento e de decrescimento de f , concavidades e assíntotas (caso existam).

Passo 1

Bom, primeiro vamos pensar em domínio: a única restrição ali é o ln ⁡ x que força x a ser maior que 0 . Assim, temos:

D o m : x ∈   ] 0 , + ∞ [

Ok, não havendo outras restrições vamos utilizar os limites de f em 0 e + ∞ para tentar achar assíntotas:

lim x → 0 + ⁡ 3 x + ln ⁡ x x = 3 0 + - ∞ 0 = - ∞

Assíntota vertical em x = 0 .

lim x → + ∞ ⁡ 3 x + ln ⁡ x x =

lim x → + ∞ ⁡ 3 x 2 + ln ⁡ x x → L ' H lim x → + ∞ ⁡ 6 x + 1 x 1 = + ∞

Não temos assíntotas horizontais. Vamos procurar por assíntotas oblíquas então!

m = lim x → + ∞ ⁡ f x x = lim x → + ∞ ⁡ 3 + ln ⁡ x x 2 = 3

,   p o i s   lim x → + ∞ ⁡ ln ⁡ x x 2 → L ' H lim x → + ∞ ⁡ 1 x 2 x = 0

n = lim x → + ∞ ⁡ f x - m x = lim x → + ∞ ⁡ 3 x + ln ⁡ x x - 3 x

= lim x → + ∞ ⁡ ln ⁡ x x → L ' H lim x → + ∞ ⁡ 1 / x 1 = 0

Logo, concluímos que y = 3 x é assíntota oblíqua.

Agora vamos analisar a derivada primeira e a derivada segunda:

f ' x = 3 + 1 - ln ⁡ x x 2

f ' ' x = 1 - ln ⁡ x ' x 2 - 1 - ln ⁡ x x 2 ' x 2 2

= - 1 x x 2 - 1 - ln ⁡ x 2 x x 4

= - 1 - 2 + 2 ln ⁡ x x 3

= 2 ln ⁡ x - 3 x 3

Olhando para f ' ( x ) nós reparamos que nunca é igual a 0 , olha:

f ' x = 3 + 1 - ln ⁡ x x 2 = 3 x 2 + 1 - ln ⁡ x x 2

Olha o termo de cima, é exatamente ao que provamos ser maior que 0 na letra a ! Logo, concluímos que f ' ( x ) é sempre positiva e não existem pontos críticos. Logo, a função é sempre crescente!

Observando a derivada segunda agora:

f ' ' x = 2 ln ⁡ x - 3 x 3

No intervalo do domínio temos x 3 sempre positivo. Assim, o sinal depende apenas de ( 2 ln ⁡ x - 3 ) .

2 ln ⁡ x = 3 → x = e 3 / 2

Há, portanto, um ponto de inflexão em x = e e ;   f e 3 / 2 = 3 e 3 / 2 + 1 2 e 3 / 2 e antes dele a concavidade é para baixo, depois é para cima.

Com isso podemos desenhar nosso gráfico!

Resposta

( f i g u r a   a c i m a )

Exercícios de Livros Relacionados

Uma partícula move-se segunda a lei do movimento s = f ( t ) , t ≥ 0 , em que t é medido em segundos e s em metrosEncontre a velocidade no instante t Qual a velocidade depois de 3 s Quando a partícula
Uma partícula move-se segunda a lei do movimento s = f ( t ) , t ≥ 0 , em que t é medido em segundos e s em metrosEncontre a velocidade no instante t Qual a velocidade depois de 3 s Quando a partícula
Esboce um gráfico da função racional dada e identifique as coordenadas dos pontos estacionários e de inflexão. Mostre as assíntotas horizontais, verticais, oblíquas e curvilíneas e dê suas equações. I
Use o roteiro desta seção para esboçar o gráfico da curva. No passo D , ache uma equação para a assíntota oblíqua. y = 2 x 3 + x 2 + 1 x 2 + 1
Mostre que a curva y = x - tan - 1 ⁡ x tem duas assíntotas oblíquas: y = x + π / 2 e y = x - π / 2 Use esse fato para esboçar a curva.