Considere a função definida por
Onde e
- Determine o valor das constantes e para que seja contínua e diferenciavel.
- Atribua às constantes a e b os valores encontrados no item anterior. Determine, caso existam:
- Faça um esboço do gráfico de e de suas assíntotas, caso existam.
b.1) As retas assíntotas horizontais do gráfico de
b.2) As retas assíntotas verticais de .
b.3) As retas assíntotas oblíquas do gráfico de .
b.4) Os intervalos de crrescimento e decrescimento de .
b.5) Os intervalos onde o gráfico de tem concavidade voltada para cima e onde tem concavidade voltada para baixo
Passo 1
Letra a) Pow, se o próprio problema nos disse que a função é continua e diferenciável, é pq ele quer que utilizamos esses detalhes. Veja só:
Se a função é contínua, então no ponto , onde ocorre a mudança de função, essas duas coisas devem ser iguais, ou seja:
Substituindo...
Ou seja
Passo 2
Por outro lado, se a função é diferenciável, então pela definição, as derivadas devem ter o mesmo valor no ponto problemático:
Deriavando primeiro, vamos obter
Substituindo agora na nossa relação
Se , então
Passo 3
Item b.1: Para determinar as assíntotas horizontais, batamos aplicar o limite dessa função no infinito positivo, e depois no infinito negativo.
Apenas lembre-se que no lado positivo, vamos trabalhar com a função e no negativo, a !:)
Como , quando
Esse limite todo vai para o infinito
Quanto ao outro lado da história, ou seja:
Colocando em evidência esse
Notasse que quando é um termo muito grande negativo, é um termo muito grande positivo, pois o produto de duas coisas negativas é algo positivo, logo
Logo, não existem assintotas horizontais.
Passo 4
Item b.2: Para determinar as assintotas verticais, devemos olhar para o dominio da função . Como essa função está definida em toda a reta, não existe nenhum ponto de com algum problema, logo podemos dizer que não existem assintotas verticais!;)
Passo 5
Item b.3: Aqui, a gente vai ter um pouquinho mais de trabalho do que as outras, mas é apenas aplicação de fórmula também!
Para verificar se existe esse tipo de assíntota devemos buscar a solução de dois limites muito parecidos com os que usamos para averiguar a existência de assíntotas horizontais:
Dividindo todos os termos de cima por
Averiguando o outro lado da coisa...
Como em cima vai para o infinito e embaixo também , podemos aplicar :
vai para o infinito, todo esse produto vai a zero, logo concluímos que
Logo, existe uma assíntota oblíqua de coeficiente angular .
Para encontrar o coeficiente linear basta fazermos:
Ou seja
Quando vai para o infinito, o arco-tangente vai para , logo
Portanto, a assíntota obliqua é
Passo 6
Item b.4: Como buscamos os intervalos de crescimento e decrescimento de , necessitamos de trabalhar com a sua derivada, ou seja:
Repare que nessa função derivada que obtemos, o denominador é um termo positivo pra qualquer , pois o menor valor que ele pode dar é , quando . Logo, todo esse termo , é positivo.
O dobro de algo positivo é ainda positivo, somando com ... Continua sempre positivo, logo sempre cresce no sei domínio:)
Passo 7
Item b.5: Analisar a concavidade é analisar a segunda derivada:
Derivando utilizando a regra da fração...
Como o denominador é sempre positivo, o sinal de depende inteiramente de . Como assume valores negativos par , também terá; quando , será positivo e também será, percebeu? Logo:
Passo 8
Letra c) Jogando todos esses ingredientes no gráfico com a atenção de que a muda de função quando , ou seja, antes de ela é uma parábola com a concavidade para cima e depois de ela é essa com concavidade para baixo e com essa assíntota obliqua, teremos:
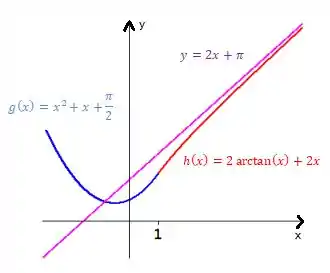
Resposta
a)
b.1) Não existem assíntotas horizontais.
b.2) Não existem assíntotas verticais.
b.3)
b.4) Crescente em todo domínio de .
b.5)
c)