A respeito das seguintes funções
I.
II.
Determine:
a) Domínio;
b) Intersecções com os eixos (explicitar as raízes);
c) Assíntotas, caso existam;
d) Intervalos de crescimento ou decrescimento;
e) Pontos de máximo ou mínio locais e absolutos da função, e os respectivos valores da função nesses pontos;
f) Concavidade e ponto de inflexão;
g) Use as informações dos itens (a-f) para esboçar o gráfico da função.
Passo 1
Fala galerinha, beleza? Bora esboçar uns gráficos?
Esse é aquele tipo de problema super tradicional de seguir o roteiro e esboçar o gráfico das funções. Vamos começar pela primeira função
A única restrição do domínio é que o denominador não pode se anular, de modo que
Portanto,
Como , a função não intercepta o eixo (vertical). Para achar as raízes, fazemos
Portanto,
Essa equação não tem solução real, de modo que a função não apresenta raízes, isto é, não corta o eixo .
Passo 2
Agora vamos verificar se apresenta assíntotas. Para isso, vamos lembrar um pouquinho das assíntotas oblíquas do tipo . O coeficiente angular é encontrada fazendo
Como o limite é finito, a função apresenta esse tipo de assíntota! Vale destacar que para obtemos o mesmo resultado:
Para achar o coeficiente linear , fazemos
O mesmo acontece para . Desta forma, tanto para como para , o gráfico de apresenta uma assíntota oblíqua cuja equação é
Vamos ver o que acontece quando . Pela direita, temos
Pela esquerda:
Vemos que a reta corresponde a uma assíntota vertical do gráfico da função!
Passo 3
Para analisar os intervalos de crescimento e decrescimento, temos que derivar a função:
Os pontos críticos ocorrem quando :
Desta forma, podemos construir o varal:
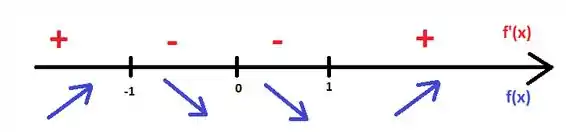
Vemos que a função é crescente nos intervalos e , e decrescente nos intervalos e .
Como a função explode para (ver assíntotas), ela não apresenta máximos ou mínimos globais, mas pode apresentar locais!
Repare que em , a função cresce antes e decresce depois, correspondendo a um máximo local. Já em ocorre o inverso, correspondendo a um mínimo local. Observe que
Passo 4
Vamos olhar agora para a concavidade e, para isso, tomamos a segunda derivada:
Portanto, o sinal de controla o sinal de . Para , temos , de modo que nessa região a curva é concava para cima (feliz). Já para , temos com a concavidade sendo para baixo (triste). Observe que não existe ponto em que , de modo que a função não apresenta pontos de inflexão.
De posse de todas essas informações podemos esboçar o gráfico da função:
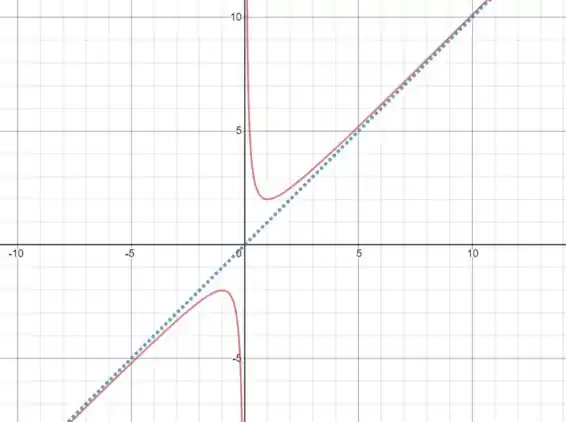
Em pontilhado desenhei a assíntota oblíqua . Observe os pontos de máximo e mínimo locais, intervalos de crescimento e decrescimento, bem como a concavidade em cada região. Note também que a curva não corta nenhum dos eixos.
Passo 5
Ufa, finalizamos a discussão da primeira função. Agora vamos partir para a segunda:
Como nunca se anula, não temos restrição nenhuma quanto aos valores que pode assumir, de modo que o domínio de é real:
Para achar a interseção com o eixo , fazemos :
Já para achar a interseção com o eixo (raiz):
Além disso,
Isso significa que as assíntotas no infinito são horizontais, mais precisamente a reta
Passo 6
Agora derivamos usando a regra do quociente:
Os pontos críticos ocorrem quando :
Logo, temos dois pontos críticos:
Considerando que , o sinal de é determinado pelo numerador , que corresponde a uma função do segundo grau. Com isso, é fácil fazer o varal:
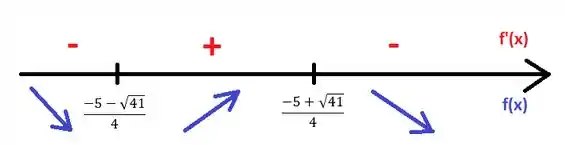
A função é decrescente nos intervalos e , e crescente no intervalo .
Como a função tende a quando , os pontos de máximo e mínimo locais correspondem aos máximo e mínimo globais! O máximo ocorre em
Já o mínimo:
Passo 7
Estamos quase terminando, falta só olhar para a segunda derivada:
Logo,
O denominador é sempre positivo de modo que o denominador controla o sinal da função! A seguir faço um varal considerando as raízes do polinômio:

Eu usei uma calculadora gráfica para achar as raízes do polinômio já que isso não é uma tarefa tão trivial de ser feita a mão. Vale lembrar que essa prova foi feita à distância num contexto de pandemia, então esses recursos estavam disponíveis! Numa prova presencial isso seria impraticável.
Agora só resta fazer o esboço do gráfico e fechamos o problema:
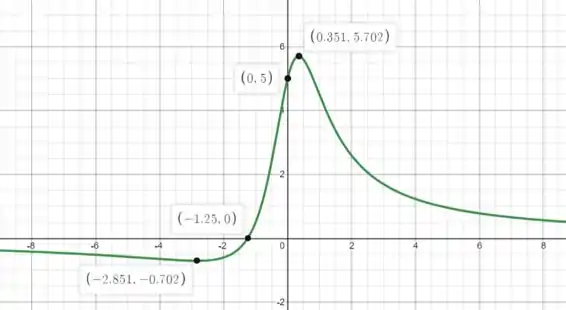
Resposta
não intercepta os eixos
assíntota de para :
é crescente em
é decrescente em
máximo local:
mínimo local:
é concava para cima para e concava para baixo quando
interseções de com os eixos: e
assíntota de para :
é crescente para
é decrescente para e
máximo global:
mínimo global:
é concava para cima quando e
é concava para baixa quando e