UFES – Cálculo 1 – Listas de Estudos UFES – Lista 2
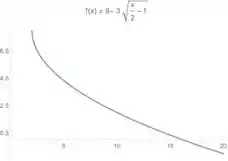
Esboce os gráficos das funções dos exercícios 12. a 17.
12.
Passo 1
Fala aí pessoal, tudo certinho??O problema está nos pedindo para fazer o esboço da função
No fundo ele quer ver como que o gráfico dessa função se comporta, ele não quer nada suuuuper preciso, a gente só precisa marcar a estrutura principal daquele gráfico, ok?A ideia nesse problema é a gente partir de uma função que já conhecemos a cara do gráfico e ir fazendo transformações em cima desse gráfico para a gente obter a cara da nossa função.
A como tem uma raiz ali, a gente vai fazer uso do gráfico de que tem essa cara aqui: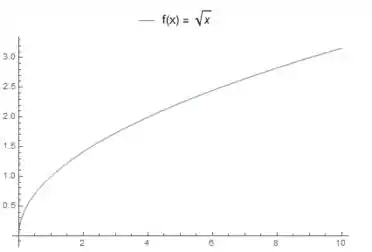
Então vamos lá ver quais tipos de transformações a gente tem que fazer nesse gráfico para ele se tornar a função do nosso problema
Passo 2
Vamos começar observando que na função desejada
Temos um sinal negativo antes da raiz, então a gente já sabe que a primeira transformação no gráfico de é espelhar esse gráfico em relação ao eixo , assim ó:
E aquele ali? Bom, o papel dele é só aumentar em 3 vezes os valores desse gráfico aqui de cima. Por exemplo, onde tem seria . Isso não altera muito a cara do nosso gráfico, já que a gente não está tão preocupado nos números em si.
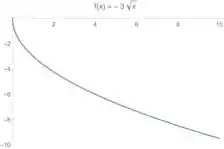Show!!
Passo 3
Uma outra coisa que a gente pode perceber é que tem um somado à essa raiz, certo? Então a gente tem uma transformação do tipo:
Esse tipo de tipo de transformação só desloca o nosso gráfico um número de unidades para cima (ao longo do eixo ). Então temos que andar o último gráfico que a gente obteve unidades para cima. Ele fica assim ó:
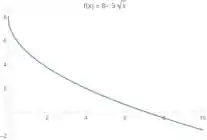
Beleza! Agora a gente tem que alterar a cara de !
Passo 4
Até agora a gente conseguiu o gráfico de
Mas queremos o gráfico de
A primeira coisa que podemos observar é que o passa a ser certo? Esse tipo de transformação:
Estica horizontalmente o gráfico, então a gente tem:
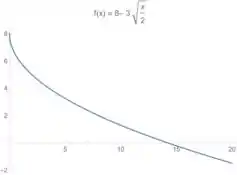
Passo 5
Por fim, observamos que temos uma transformação do tipo:
Que no gráfico funciona como o deslocamento horizontal da função para a direita unidades.Mas cuidadooo!!
O que a gente passa a ter é
E olha o que acontece se pegarmos valores de menores que ... Vamos ter uma raiz quadrada de números negativos!! Então a função, agora, não existe para valores de . Então temos o seguinte gráfico:
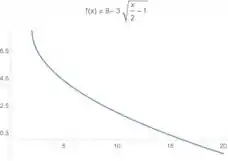
Como ele só quer um esboço, a gente resolveu essa 😊 Vamos para a próxima??
Resposta
