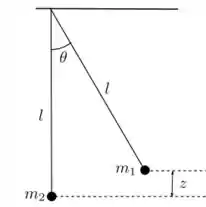
Considere dois pêndulos simples, de mesmo comprimento presos a um mesmo ponto como mostra a figura. A partícula de massa é solta do repouso a uma altura em relação a posição de equilíbrio e atinge a partícula de massa em Anteriormente, a partícula de massa estava em repouso, na posição de equilíbrio. Após a colisão as duas partículas permanecem juntas. Considere a aceleração da gravidade conhecida e que, tanto antes quanto depois da colisão, vale a aproximação de pequenos ângulos para ambos os pêndulos.
- Calcule a frequência angular do sistema após a colisão.
- Obtenha as condições inicias do sistema em
- Calcule a amplitude do sistema após a colisão.
Passo 1
a):
Bom, galera, antes da gente usar os conhecimentos de física 2 aqui, nós vamos precisar lembrar um pouco de fisica1.
Pra que? Pra saber qual é velocidade que tem quando atinge . E depois disso, precisamos descobrir qual a velocidade que os dois corpos tem ao seguirem juntos.
Beleza?
Bem, vamos lá:
A massa tem uma energia potencial gravitacional associada a ela no inicio do problema que é dada por:
Quando ela desce toda a altura , essa energia se transforma em energia cinética, então:
Agora a gente precisa usar a conservação do momento. Como a colisão é inelástica e as partículas seguem juntas, então:
Essa velocidade é velocidade inicial do movimento oscilatório:
Passo 2
Opa, mas que movimento oscilatório? Bom, como a gente viu na teoria, o movimento de um pêndulo simples pode ser aproximado por um MHS assim:
Pela segunda lei de Newton:
De novo, vamos usar a aproximação para pequenos valores de :
Logo:
Então:
Passo 3
b):
Bom, a gente vai considerar que o sistema sai da posição Então:
E quanto a:
Bom, como vimos, a velocidade inicial é:
Mas o nosso MHS tá lidando com ângulos pow! E qual a relação entre uma velocidade angular e uma linear? Assim:
Então:
Ou, se a gente considerar que o sentido positivo é oposto da velocidade das bolinhas:
Passo 4
c):
A solução geral pra EDO do MHS é:
A gente quer achar Mas se a gente usar as condições inicias do item anterior:
E a derivada nos dá:
E a condição inicial é:
Como a velocidade é negativa e tem um sinal de menos na frente da equação, a fase tem que ser positiva:
Então:
Resposta
a):
b):
c):