Em que ponto do movimento de um pêndulo simples a tração no fio atinge o valor máximo? E o valor mínimo?
Passo 1
Lembra do pêndulo simples? É esse camarada aqui:
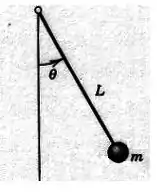
E como as forças se decompõem? Dá uma olhada nessa figura:
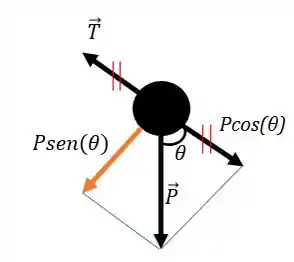
E como não tem movimento na direção do fio, podemos dizer que:
Passo 2
Bom, se a tração é proporcional ao cosseno do ângulo, quando ela vai ser máxima? Quando o cosseno for máximo né, ou seja, quando:
Então a tração vai ser máxima quando for igual a zero, ou seja, quando o pêndulo estiver na posição vertical.
Passo 3
Usando o mesmo raciocínio, quando a tração vai ser mínima? Quando o cosseno for mínimo também!
Lembrando que o cosseno é decrescente no primeiro quadrante (ou seja, de zero a 90 graus, quanto maior o ângulo menor o cosseno) o cosseno vai ser mínimo quando for máximo!
O ângulo máximo é sempre o ângulo da posição em que o pêndulo foi abandonado.
“Mas como eu acho esse ângulo?”
Então, o problema pode te dar a posição usando e não x, tipo assim:
E aí no caso o seu ângulo máximo vai ser .
Entãããooo....ele pode te dar a altura h de onde o pêndulo foi abandonado, tipo assim:
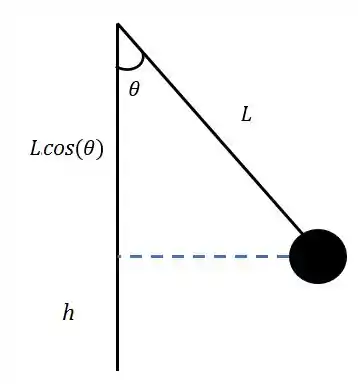
Nesse caso você vai usar a relação:
Passo 4
Resumindo, tração máxima:
Tração mínima:
Resposta
Tração máxima:
Tração mínima: