Um pêndulo simples, como mostrado na figura, é lançado de uma posição , com uma velocidade .
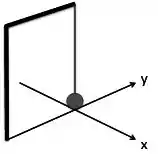
Qual é a trajetória do pêndulo, vista de cima, dados e positivos?
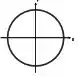 sentido anti-horário
sentido anti-horário
 sentido horário
sentido horário
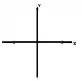
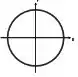 sentido horário
sentido horário
 sentido anti-horário
sentido anti-horário
Passo 1
Bem, quando um pêndulo é solto de uma posição , sabemos que ele vai oscilar entre e . Saindo de para no inicio.
Como foi adicionado uma velocidade inicial em , sabemos que o primeiro movimento será da direita par esquerda e de baixo para cima, dessa forma no sentido anti-horário.
E ainda, sabemos que como não há ação de uma força dissipativa, a energia mecânica deve ser conservada. Então não é possível que ele assuma posições maiores que , sendo assim, eliminamos as elipses, e chegamos que a alternativa correta é a
Resposta
Alternativa